题目内容
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 , 都有
, 都有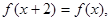 且当
且当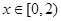 时,
时, 的值为 .
的值为 .
【答案】
1
【解析】解:对于对于 ,都有
,都有 所以函数的周期为2,因为函数
所以函数的周期为2,因为函数
 是
是 上的偶函数,当
上的偶函数,当 时,
时,
= 
故答案为1

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
题目内容
已知函数 是
是 上的偶函数,若对于
上的偶函数,若对于 , 都有
, 都有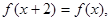 且当
且当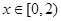 时,
时, 的值为 .
的值为 .
1
【解析】解:对于对于 ,都有
,都有 所以函数的周期为2,因为函数
所以函数的周期为2,因为函数
 是
是 上的偶函数,当
上的偶函数,当 时,
时,
= 
故答案为1

 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案