题目内容
已知函数 是
是 上的偶函数,满足
上的偶函数,满足 ,当
,当 时,
时, ,则( )
,则( )
A. B.
B.
C.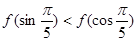 D.
D.
【答案】
D
【解析】
试题分析:当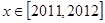 时,
时,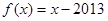 ,即函数
,即函数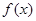 在
在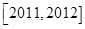 上单调递增,由
上单调递增,由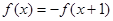 可得
可得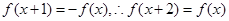 ,即函数
,即函数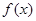 的周期为2,所以函数
的周期为2,所以函数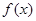 在
在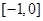 上单调递增,又因为函数
上单调递增,又因为函数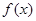 是
是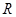 上的偶函数,所以函数
上的偶函数,所以函数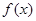 在
在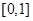 上单调递减,而
上单调递减,而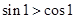 ,所以
,所以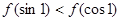 .
.
考点:本小题主要考查函数的奇偶性、周期性、单调性的判断和应用,考查学生对问题的分析和应用能力以及转化问题的能力.
点评:对于此类问题,关键是根据题意找出函数的周期,然后画出函数的简图,数形结合解决问题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 是
是 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有 成立,当
成立,当 且
且 时,都有
时,都有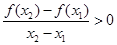 给出下列命题:
给出下列命题: 且
且 是函数
是函数 的一个周期;②直线
的一个周期;②直线 是函数
是函数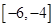 上是增函数; ④函数
上是增函数; ④函数 上有四个零点.其中正确命题的序号为 (把所有正确命题的序号都填上)
上有四个零点.其中正确命题的序号为 (把所有正确命题的序号都填上) 是
是 上的偶函数,且
上的偶函数,且 在
在 上是减函数,若
上是减函数,若 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 是
是 上的偶函数,对任意
上的偶函数,对任意 ,都有
,都有 成立,
成立, 且
且 时,都有
时,都有 给出下列命题:
给出下列命题: 且
且 是函数
是函数 的一个周期;
的一个周期; 是函数
是函数 上是增函数;
上是增函数; 上有四个零点.
上有四个零点.