题目内容

已知曲线C1的极坐标方程为ρ2cos2θ=8，曲线C2的极坐标方程为θ=
π
6
，曲线C1、C2相交于A、B两点．（p∈R）
（Ⅰ）求A、B两点的极坐标；
（Ⅱ）曲线C1与直线
x=1+
3
2
t
y=
1
2
t
（t为参数）分别相交于M，N两点，求线段MN的长度．
分析：（I）由
ρ2cos2θ=8
θ=
π
6
得：ρ2cos
π
3
=8，即可得到ρ．进而得到点A，B的极坐标．
（II）由曲线C1的极坐标方程ρ2cos2θ=8化为ρ2（cos2θ-sin2θ）=8，即可得到普通方程为x2-y2=8．将直线
x=1+
3
2
t
y=
1
2
t
代入x2-y2=8，整理得t2+2
3
t-14=0．进而得到|MN|．
解答：解：（Ⅰ）由
ρ2cos2θ=8
θ=
π
6
得：ρ2cos
π
3
=8，
∴ρ2=16，
即ρ=±4．
∴A、B两点的极坐标为：A(4，
π
6
)，B(-4，
π
6
)或B(4，
7π
6
)．
（Ⅱ）由曲线C1的极坐标方程ρ2cos2θ=8化为ρ2（cos2θ-sin2θ）=8，
得到普通方程为x2-y2=8．
将直线
x=1+
3
2
t
y=
1
2
t
代入x2-y2=8，
整理得t2+2
3
t-14=0．
∴|MN|=
(2
3
)2-4×(-14)
1
=2
17
．
点评：本题考查了极坐标与直角坐标的互化公式、此时方程化为普通方程、弦长公式等基础知识与基本技能方法．
练习册系列答案
相关题目
已知曲线C1的极坐标方程为P=6cosθ，曲线C2的极坐标方程为θ=
π4
（p∈R），曲线C1，C2相交于A，B两点．
（Ⅰ）把曲线C1，C2的极坐标方程转化为直角坐标方程；
（Ⅱ）求弦AB的长度．
（2012•香洲区模拟）已知曲线C1的极坐标方程为ρ=6cosθ，曲线C2的极坐标方程为θ=
π
4
(ρ∈R)，曲线C1、C2相交于点A、B．则弦AB的长等于
3
2
3
2
．
极坐标系的极点是直角坐标系的原点，极轴为x轴正半轴．已知曲线C1的极坐标方程为ρ=2cosθ，曲线C2的参数方程为
x=2+tcosα
y=
3
+tsinα
(其中t为参数，α为字母常数且α∈[0，π))
（1）求曲线C1的直角坐标方程和曲线C2的普通方程；
（2）当曲线C1和曲线C2没有公共点时，求α的取值范围．
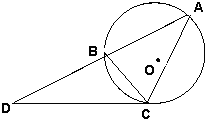（1）圆O是△ABC的外接圆，过点C的圆的切线与AB的延长线交于点D，CD=2
7
，AB=BC=3，求BD以及AC的长．
（2）已知曲线C1的极坐标方程为ρ=6cosθ，曲线C2的极坐标方程为θ=
π
4
，曲线C1，C2相交于A，B两点
（I）把曲线C1，C2的极坐标方程转化为直角坐标方程；
（II）求弦AB的长度．
（3）已知a，b，c都是正数，且a，b，c成等比数列，求证：a2+b2+c2＞（a-b+c）2．
设极点与原点重合，极轴与x轴正半轴重合．已知曲线C1的极坐标方程是：ρcos(θ+
π
3
)=m，曲线C2参数方程为：
x=2+2cosθ
y=2sinθ
（θ为参数），若两曲线有公共点，则实数m的取值范围是
[-1，3]
[-1，3]
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网