题目内容
设极点与原点重合,极轴与x轴正半轴重合.已知曲线C1的极坐标方程是:ρcos(θ+
)=m,曲线C2参数方程为:
(θ为参数),若两曲线有公共点,则实数m的取值范围是
| π |
| 3 |
|
[-1,3]
[-1,3]
.分析:将两曲线方程化为直角坐标方程,根据题意可得圆心到直线的距离小于或等于半径,即
≤2,由此求得
实数m的取值范围.
| |2-2m| |
| 2 |
实数m的取值范围.
解答:解:将两曲线方程化为直角坐标方程,得C1:x-
y-2m=0,C2:(x-2)2+y2=4.
因为两曲线有公共点,所以,圆心到直线的距离小于或等于半径,即
≤2,
解得-1≤m≤3,故m∈[-1,3],
故答案为:[-1,3].
| 3 |
因为两曲线有公共点,所以,圆心到直线的距离小于或等于半径,即
| |2-2m| |
| 2 |
解得-1≤m≤3,故m∈[-1,3],
故答案为:[-1,3].
点评:本题考查把极坐标方程化为直角坐标方程的方法,点到直线的距离公式的应用,得到
≤2,是解题的关键.
| |2-2m| |
| 2 |

练习册系列答案
相关题目
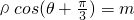 ,曲线C2参数方程为:
,曲线C2参数方程为: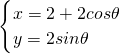 (θ为参数),若两曲线有公共点,则实数m的取值范围是________.
(θ为参数),若两曲线有公共点,则实数m的取值范围是________.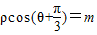 ,曲线C2参数方程为:
,曲线C2参数方程为: (θ为参数),若两曲线有公共点,则实数m的取值范围是 .
(θ为参数),若两曲线有公共点,则实数m的取值范围是 .