题目内容
(本题满分14分)如图,在正方体ABCD-A1B1C1D1中,E、F为棱AD、AB的中点.

(1)求证:EF∥平面CB1D1;
(2)求证:平面CAA1C1⊥平面CB1D1.
【答案】
(1)连结BD.在长方体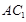 中,对角线
中,对角线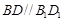 .又
.又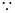 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点, 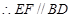 .
. 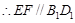 . 又B1D1
. 又B1D1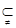 平面
平面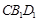 ,
,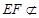 平面
平面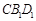 ,
, EF∥平面CB1D1.(2)因为
在长方体
EF∥平面CB1D1.(2)因为
在长方体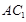 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1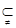 平面A1B1C1D1,
平面A1B1C1D1,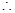 AA1⊥B1D1.又因为在正方形A1B1C1D1中,A1C1⊥B1D1,
AA1⊥B1D1.又因为在正方形A1B1C1D1中,A1C1⊥B1D1,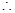 B1D1⊥平面CAA1C1. 又因为B1D1
B1D1⊥平面CAA1C1. 又因为B1D1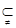 平面CB1D1,
平面CB1D1,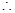 平面CAA1C1⊥平面CB1D1
平面CAA1C1⊥平面CB1D1
【解析】
试题分析:(1)证明:连结BD.在长方体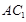 中,对角线
中,对角线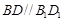 .
.
又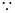 E、F为棱AD、AB的中点,
E、F为棱AD、AB的中点, 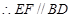 .
.
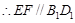 . 又B1D1
. 又B1D1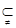 平面
平面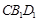 ,
,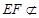 平面
平面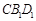 ,
,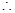 EF∥平面CB1D1.
EF∥平面CB1D1.
(2)因为
在长方体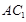 中,AA1⊥平面A1B1C1D1,而B1D1
中,AA1⊥平面A1B1C1D1,而B1D1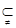 平面A1B1C1D1,
平面A1B1C1D1,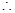 AA1⊥B1D1.又因为在正方形A1B1C1D1中,A1C1⊥B1D1,
AA1⊥B1D1.又因为在正方形A1B1C1D1中,A1C1⊥B1D1,
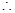 B1D1⊥平面CAA1C1. 又因为B1D1
B1D1⊥平面CAA1C1. 又因为B1D1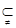 平面CB1D1,
平面CB1D1,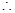 平面CAA1C1⊥平面CB1D1
平面CAA1C1⊥平面CB1D1
考点:本题考查了空间中的线面关系
点评:证明立体几何问题常常利用几何方法,通过证明或找到线面之间的关系,依据判定定理或性质进行证明求解

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目


 、
、 的边长都是1,平面
的边长都是1,平面 平面
平面 在
在 上移动,点
上移动,点 在
在 上移动,若
上移动,若 (
( )
)
 的长;
的长; 为何值时,
为何值时, 与面
与面 所成锐二面角余弦值的大小.
所成锐二面角余弦值的大小. ,又E、F分别是C1A和C1B的中点。
,又E、F分别是C1A和C1B的中点。 (1)求证:EF//平面ABC;
(1)求证:EF//平面ABC; 平面C1CBB1;
平面C1CBB1;