题目内容
【题目】已知椭圆![]() :
: ![]() 的离心率
的离心率![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,
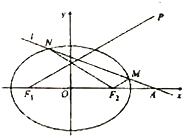
, ![]() ,点
,点![]() 满足:
满足: ![]() 在线段
在线段![]() 的中垂线上.
的中垂线上.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若斜率为![]() (
(![]() )的直线
)的直线![]() 与
与![]() 轴、椭圆
轴、椭圆![]() 顺次相交于点
顺次相交于点![]() 、
、![]() 、
、![]() ,且
,且![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)
【解析】试题分析:(1)由![]() 在线段
在线段![]() 的中垂线上得
的中垂线上得![]()
![]() ,代入点坐标得
,代入点坐标得![]() ,解得
,解得![]() ,再根据
,再根据![]() ,得
,得![]() ,
, ![]() ,(2)由
,(2)由![]() ,得
,得![]() ,设
,设![]() ,代入化简得
,代入化简得![]() ,
, ![]() ,即
,即![]() ,再利用直线
,再利用直线![]() 方程与抛物线方程联立方程组,结合韦达定理及判别式恒大于零得
方程与抛物线方程联立方程组,结合韦达定理及判别式恒大于零得![]() ,
, ![]() ,且
,且![]() .
.
试题解析:(Ⅰ)椭圆![]() 的离心率
的离心率![]() ,
,
得![]() ,其中
,其中![]() ,椭圆
,椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
, ![]() ,
,
又点![]() 在线段
在线段![]() 的中垂线上,∴
的中垂线上,∴![]()
![]() ,∴
,∴![]() ,
,
解得![]() ,
, ![]() ,
, ![]() ,
,
∴椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)由题意,直线![]() 的方程为
的方程为![]() ,且
,且![]() ,联立
,联立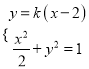 ,
,
得![]() ,
,
由![]() ,得
,得![]() ,且
,且![]() .
.
设![]() ,则有
,则有![]() ,
, ![]() (
(![]() )
)
∵![]() ,且由题意
,且由题意![]() ,
,
![]() , 又
, 又![]()
![]() ,
, ![]() ,
, 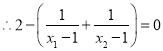 ,
,
整理得![]() ,
,
将(![]() )代入得,
)代入得, ![]()
![]() , 知此式恒成立,
, 知此式恒成立,
故直线![]() 斜率
斜率![]() 的取值范围是
的取值范围是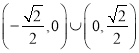 .
.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案
相关题目