题目内容
【题目】如图，我海监船在
岛海域例行维权巡航，某时刻航行至
处，此时测得其东北方向与它相距32海里的
处有一外国船只，且
岛位于海监船正东
海里处．
（1）求此时该外国船只与
岛的距离；
（2）观测中发现，此外国船只正以每小时8海里的速度沿正南方向航行，为了将该船拦截在离
岛24海里处，不让其进入
岛24海里内的海域，试确定海监船的航向，并求其速度的最小值．（参考数据： 
）
【答案】（1）
；（2）
.
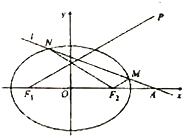
【解析】试题分析：（1）直接利用余弦定理，求得距离为
；（2）过点
作
于点
，连结
，利用勾股定理和正弦的概念，求得
，故海监船的航向为北偏东
，同时，外国船只到达点
的时间
（小时），海监船的速度
.
试题解析：
（1）依题意，在
中， 
，
由余弦定理得
，
∴
．．．．．．．．．．．．．．．．．．．．．．．．．．．．4分
即此时该外国船只与
岛的距离为
海里．．．．．．．．．．．．．．．．．．．．．5分
（2）过点
作
于点
，
在
中， 
，∴
，．．．．．．．．．．6分
以
为圆心，24为半径的圆交
于点
，连结
，
在
中， 
，∴
．．．．．．．．．．．．．．．．．7分
又
，
∴
．．．．．．．．．．．．．．．．．9分
外国船只到达点
的时间
（小时）
∴海监船的速度
（海里/小时）．．．．．．．．．．．．．．．．．．11分
故海监船的航向为北偏东
，速度的最小值为40海里/小时．．．．．．．．．．12分
时刻准备着暑假作业原子能出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
【题目】某房屋开发公司根据市场调查，计划在2017年开发的楼盘中设计“特大套”、“大套”、“经济适
用房”三类商品房,每类房型中均有舒适和标准两种型号.某年产量如下表:
房型 | 特大套 | 大套 | 经济适用房 |
舒适 | 100 | 150 |
|
标准 | 300 |
| 600 |
若按分层抽样的方法在这一年生产的套房中抽取50套进行检测,则必须抽取“特大套”套房10套, “大套”15套.
(1)求
,
的值;
(2)在年终促销活动中,奖给了某优秀销售公司2套舒适型和3套标准型“经济适用型”套房，该销售公司又从中随机抽取了2套作为奖品回馈消费者.求至少有一套是舒适型套房的概率;
(3)今从“大套”类套房中抽取6套,进行各项指标综合评价,并打分如下:
现从上面6个分值中随机的一个一个地不放回抽取,规定抽到数9.6或9.7,抽取工作即停止.记在抽取到数9.6或9.7所进行抽取的次数为
,求的分布列及数学期望.
