题目内容
现需要制作一个容积为32 的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?
的有铝合金盖的圆柱形铁桶,已知单位面积铝合金的价格是铁的3倍,问底面半径多大时桶的总造价最小?
解:r=2时,总造价最低.
解析试题分析:根据题意,设底面半径为r,由于该容器是一个容积为32 的有铝合金盖的圆柱形铁桶,那么可知V=
的有铝合金盖的圆柱形铁桶,那么可知V=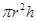 =32,同时那么高度为
=32,同时那么高度为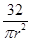 ,那么圆柱的侧面积为
,那么圆柱的侧面积为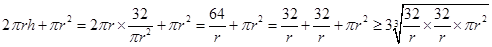 ,当且仅当r=2时取得最小值,故可知总造价最低的时候,半径为2。
,当且仅当r=2时取得最小值,故可知总造价最低的时候,半径为2。
考点:函数运用
点评:解决的关键是利用底面半径表示出表面积来求解最值,属于中档题。

练习册系列答案
相关题目
石家庄市为鼓励居民节约用电,采用分段计费的方法计算电费,每月用电不超过100度时,按每度0.52元计算,每月用电量超过100度时,其中的100度仍按原标准收费,超过的部分每度按0.6元计算.
(1)设月用电 度时,应缴电费
度时,应缴电费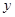 元,写出
元,写出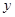 关于
关于 的函数关系式;
的函数关系式;
(2)小明家第一季度缴纳电费情况如下:
| 月份 | 一月 | 二月 | 三月 | 合计 |
| 缴费金额 | 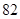 元 元 | 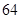 元 元 | 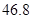 元 元 | 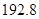 元 元 |
 ,且曲线
,且曲线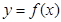 斜率最小的切线与直线
斜率最小的切线与直线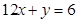 平行.求:(1)
平行.求:(1) 的值;(2)函数
的值;(2)函数 的单调区间.
的单调区间.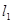 表示神风摩托车厂一天的销售收入与摩托车销售量的关系;
表示神风摩托车厂一天的销售收入与摩托车销售量的关系;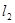 表示摩托车厂一天的销售成本与销售量的关系.
表示摩托车厂一天的销售成本与销售量的关系.
 和
和 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
 分别对应哪一个函数?
分别对应哪一个函数? ,且
,且 ,指出
,指出 的值,并说明理由;
的值,并说明理由;

 、纵边
、纵边 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
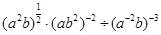 ; (2)计算:
; (2)计算: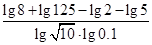 .
.  元/千克,政府补贴为
元/千克,政府补贴为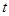 元/千克,根据市场调查,当
元/千克,根据市场调查,当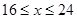 时,这种食品市场日供应量
时,这种食品市场日供应量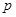 万千克与市场日需量
万千克与市场日需量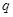 万千克近似地满足关系:
万千克近似地满足关系: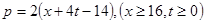 ,
,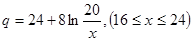 。当
。当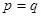 市场价格称为市场平衡价格。
市场价格称为市场平衡价格。