题目内容
数列{an}的前n项和记为Sn,已知a1=1,an+1=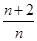 Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明:
(1)数列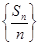 是等比数列;
是等比数列;
(2)Sn+1=4an.
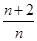 Sn(n=1,2,3,…),证明:
Sn(n=1,2,3,…),证明:(1)数列
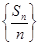 是等比数列;
是等比数列;(2)Sn+1=4an.
(1)见解析(2)见解析
(1)∵an+1=Sn+1-Sn,an+1=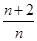 Sn(n=1,2,3,…),∴(n+2)Sn=n(Sn+1-Sn),
Sn(n=1,2,3,…),∴(n+2)Sn=n(Sn+1-Sn),
整理得nSn+1=2(n+1)Sn,∴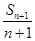 =2·
=2·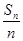 ,即
,即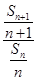 =2,∴数列
=2,∴数列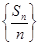 是等比数列.
是等比数列.
(2)由(1)知: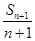 =4·
=4·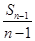 (n≥2),于是Sn+1=4·(n+1)·
(n≥2),于是Sn+1=4·(n+1)·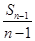 =4an(n≥2).又a2=3S1=3,∴S2=a1+a2=1+3=4a1,∴对一切n∈N*,都有Sn+1=4an.
=4an(n≥2).又a2=3S1=3,∴S2=a1+a2=1+3=4a1,∴对一切n∈N*,都有Sn+1=4an.
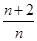 Sn(n=1,2,3,…),∴(n+2)Sn=n(Sn+1-Sn),
Sn(n=1,2,3,…),∴(n+2)Sn=n(Sn+1-Sn),整理得nSn+1=2(n+1)Sn,∴
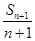 =2·
=2·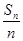 ,即
,即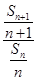 =2,∴数列
=2,∴数列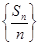 是等比数列.
是等比数列.(2)由(1)知:
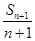 =4·
=4·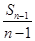 (n≥2),于是Sn+1=4·(n+1)·
(n≥2),于是Sn+1=4·(n+1)·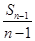 =4an(n≥2).又a2=3S1=3,∴S2=a1+a2=1+3=4a1,∴对一切n∈N*,都有Sn+1=4an.
=4an(n≥2).又a2=3S1=3,∴S2=a1+a2=1+3=4a1,∴对一切n∈N*,都有Sn+1=4an.
练习册系列答案
相关题目
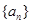 满足
满足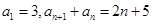 .
.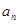 的表达式;
的表达式;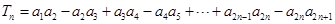 ,求
,求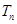 .
.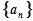 的前
的前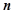 项和为
项和为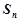 ,
,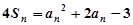 ,若
,若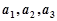 成等比数列,且
成等比数列,且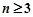 时,
时,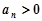 .
.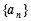 成等差数列;
成等差数列;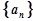 的前n项和
的前n项和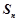 .
. 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有
 为常数,且
为常数,且 .
. ,数列
,数列 满足
满足
 ,
, ,求数列
,求数列 的通项公式;
的通项公式; 的前
的前 .
.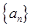 中,
中,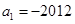 ,其前
,其前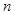 项和为
项和为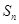 ,若
,若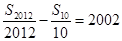 ,则
,则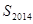 的值等于( )
的值等于( )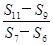 =________.
=________.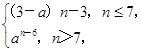 且数列{an}是递增数列,则实数a的范围是__________.
且数列{an}是递增数列,则实数a的范围是__________. 是等比数列,数列
是等比数列,数列 是等差数列,则
是等差数列,则 的值为 .
的值为 .