题目内容
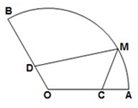 如图,点M为扇形AOB的弧的四等分点即
如图,点M为扇形AOB的弧的四等分点即 |
| AM |
| 1 |
| 4 |
 |
| AB |
4-
|
4-
|
分析:如图,连结OM,设OC=a,则OD=1-a,∠AOC=30°,∠MOD=90°,利用余弦定理求得MC,利用勾股定理求得MD,可得MC+MD,再根据两点间的距离公式求得MC+MD的最小值.
解答: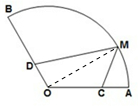 解:如图所示:连结OM,设OC=a,则OD=1-a,∠AOC=
解:如图所示:连结OM,设OC=a,则OD=1-a,∠AOC=
×120°=30°,∠MOD=90°.
由余弦定理可得:MC=
=
,
∴MD=
=
.
由于
,表示点(a,0)到点(
,
)和点(1,-1)的距离之和,
故有
,可得MC+MD的最小值为
,
故答案为:
.
 解:如图所示:连结OM,设OC=a,则OD=1-a,∠AOC=
解:如图所示:连结OM,设OC=a,则OD=1-a,∠AOC=| 1 |
| 4 |
由余弦定理可得:MC=
| a2+12-2×1×a×cos30° |
(a-
|
∴MD=
| (1-a)2+1 |
| (a-1)2+1 |
由于
|
| ||
| 2 |
| 1 |
| 2 |
故有
|
4-
|
故答案为:
4-
|
点评:本题主要考查余弦定理、两点间的距离公式的应用,属于中档题.

练习册系列答案
相关题目
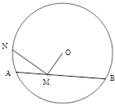 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=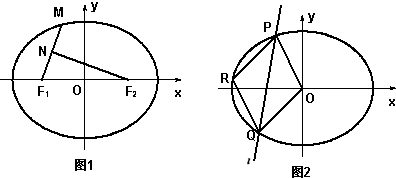
 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.
