题目内容
（几何证明选讲选做题）如图，点M为⊙O的弦AB上的一点，连接MO．MN⊥OM，MN交圆于N，若MA=2，MB=4，则MN= ．
【答案】分析：连接NM并延长交圆于P，由MN⊥OM得出M为NP中点，根据圆的相交弦定理，AM•MB=MN•NP=NP2，代入数据求解即可．
解答：解：连接NM并延长交圆于P，
∵MN⊥OM，即NP⊥OM，根据圆的相交弦定理，AM•MB=MN•NP，即2×4=MN2，MN=
故答案为：
点评：本题考查与圆有关的比例线段，要善于寻找有关线段的数量关系，结合相关性质、定理求解．
解答：解：连接NM并延长交圆于P，
∵MN⊥OM，即NP⊥OM，根据圆的相交弦定理，AM•MB=MN•NP，即2×4=MN2，MN=
故答案为：
点评：本题考查与圆有关的比例线段，要善于寻找有关线段的数量关系，结合相关性质、定理求解．
练习册系列答案
小题狂做系列答案
相关题目
（几何证明选讲选做题）
（几何证明选讲选做题）如图，四边形ABCD内接于⊙O，AB为⊙O的直径，直线MN切⊙O于D，∠MDA=60°，则∠BCD=
（考生注意：请在下列三题中任选一题作答，如果多做，则按所做的第一题评分）
（几何证明选讲选做题）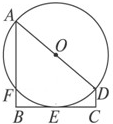
（几何证明选讲选做题）