Question

（2013•嘉兴一模）已知椭圆C：

x2

2

+y2=1的左、右焦点分别为F₁，F₂，O为原点．
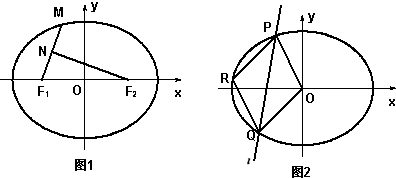
（Ⅰ）如图①，点M为椭圆C上的一点，N是MF₁的中点，且NF₂丄MF₁，求点M到y轴的距离；
（Ⅱ）如图②，直线l：y=k+m与椭圆C上相交于P，G两点，若在椭圆C上存在点R，使OPRQ为平行四边形，求m的取值范围．

Answer 1

分析：（Ⅰ）由椭圆方程求出两个焦点的坐标，设出M点的坐标，由中点坐标公式求出N点的坐标，则有两向量

F1M

，

F2N

的坐标，根据NF₂丄MF₁，由它们对应的数量积等于0即可求得M点的坐标，则点M到y轴的距离；
（Ⅱ）设出P，Q点的坐标，根据OPRQ为平行四边形，把R的坐标用P，Q点的坐标表示，然后把替换后的R的坐标代入椭圆方程(1+2k2)(x1+x2)2+8km(x1+x2)+8m2=2，再由直线方程和椭圆方程联立，利用根与系数关系求出两点P，Q的横坐标之和，代入上面的方程即可得到m与k的关系，由此可以求出m的取值范围．

解答：解：（Ⅰ）由a²=2，b²=1，所以c²=a²-b²=1，所以c=1，则F₁（-1，0），F₂（1，0）
设M（x₀，y₀），则MF₁的中点为N(

x0-1

2

，

y0

2

)，

F1M

=(x0+1，y0)，

F2N

=(

x0-3

2

，

y0

2

)．
∵MF₁⊥NF₂，∴

F1M

•

F2N

=0，即(x0+1，y0)•(

x0-3

2

，

y0

2

)=0，
∴x02-2x0-3+y02=0    （1）
又有

x02

2

+y02=1  （2）
由（1）、（2）解得x0=2-2

2

或x0=2+2

2

（舍去）
所以点M 到y轴的距离为2

2

-2．
（Ⅱ）设P（x₁，y₁）Q（x₂，y₂），
∵OPRQ为平行四边形，∴x₁+x₂=x_R，y₁+y₂=y_R．
∵R点在椭圆上，∴

xR2

2

+yR2=1，即

(x1+x2)2

2

+(y1+y2)2=1，
即

(x1+x2)2

2

+[k(x1+x2)+2m]2=1，
化简得，(1+2k2)(x1+x2)2+8km(x1+x2)+8m2=2  （3）．
由

x2 2 +y2=1 y=kx+m

，得（1+2k²）x²+4kmx+2m²-2=0．
由△＞0，得2k²+1＞m²  （4），
且x1+x2=-

4km

1+2k2

．                          
代入（3）式，得

16(1+2k2)k2m2

(1+2k2)2

-

32k2m2

1+2k2

+8m2=2，
化简得4m²=1+2k²，代入（4）式，得m≠0．
又4m²=1+2k²≥1，解得m≤-

1

2

或m≥

1

2

．

点评：本题考查了直线与圆锥曲线的关系，考查了平面向量在解析几何中的应用，训练了整体代换思想，训练了学生的计算能力，特别是（Ⅱ）中的坐标转换是解决该题的关键所在．此题属于难题．