题目内容
已知椭圆C: 的左、右焦点分别为F1,F2,O为原点.
的左、右焦点分别为F1,F2,O为原点.(I)如图①,点M为椭圆C上的一点,N是MF1的中点,且NF2丄MF1,求点M到y轴的距离;
(II)如图②,直线l::y=k+m与椭圆C上相交于P,G两点,若在椭圆C上存在点R,使OPRQ为平行四边形,求m的取值范围.

【答案】分析:(Ⅰ)由椭圆方程求出两个焦点的坐标,设出M点的坐标,由中点坐标公式求出N点的坐标,则有两向量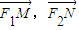 的坐标,根据NF2丄MF1,由它们对应的数量积等于0即可求得M点的坐标,则点M到y轴的距离;
的坐标,根据NF2丄MF1,由它们对应的数量积等于0即可求得M点的坐标,则点M到y轴的距离;
(Ⅱ)设出P,Q点的坐标,根据OPRQ为平行四边形,把R的坐标用P,Q点的坐标表示,然后把替换后的R的坐标代入椭圆方程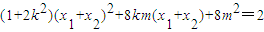 ,再由直线方程和椭圆方程联立,利用根与系数关系求出两点P,Q的横坐标之和,代入上面的方程即可得到m与k的关系,由此可以求出m的取值范围.
,再由直线方程和椭圆方程联立,利用根与系数关系求出两点P,Q的横坐标之和,代入上面的方程即可得到m与k的关系,由此可以求出m的取值范围.
解答:解:(Ⅰ)由a2=2,b2=1,所以c2=a2-b2=1,所以c=1,则F1(-1,0),F2(1,0)
设M(x,y),则MF1的中点为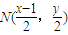 ,
,
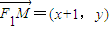 ,
,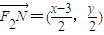 .
.
∵MF1⊥NF2,∴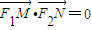 ,即
,即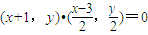 ,
,
∴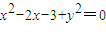 (1)
(1)
又有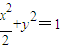 (2)
(2)
由(1)、(2)解得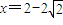 或
或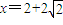 (舍去)
(舍去)
所以点M 到y轴的距离为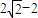 .
.
(Ⅱ)设P(x1,y1)Q(x2,y2),
∵OPRQ为平行四边形,∴x1+x2=xR,y1+y2=yR.
∵R点在椭圆上,∴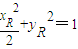 ,即
,即 ,
,
即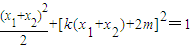 ,
,
化简得,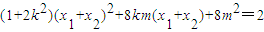 (3).
(3).
由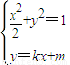 ,得(1+2k2)x2+4kmx+2m2-2=0.
,得(1+2k2)x2+4kmx+2m2-2=0.
由△>0,得2k2+1>m2 (4),
且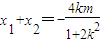 .
.
代入(3)式,得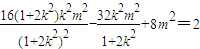 ,
,
化简得4m2=1+2k2,代入(4)式,得m≠0.
又4m2=1+2k2≥1,解得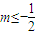 或
或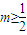 .
.
点评:本题考查了直线与圆锥曲线的关系,考查了平面向量在解析几何中的应用,训练了整体代换思想,训练了学生的计算能力,特别是(Ⅱ)中的坐标转换是解决该题的关键所在.此题属于难题.
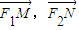 的坐标,根据NF2丄MF1,由它们对应的数量积等于0即可求得M点的坐标,则点M到y轴的距离;
的坐标,根据NF2丄MF1,由它们对应的数量积等于0即可求得M点的坐标,则点M到y轴的距离;(Ⅱ)设出P,Q点的坐标,根据OPRQ为平行四边形,把R的坐标用P,Q点的坐标表示,然后把替换后的R的坐标代入椭圆方程
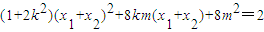 ,再由直线方程和椭圆方程联立,利用根与系数关系求出两点P,Q的横坐标之和,代入上面的方程即可得到m与k的关系,由此可以求出m的取值范围.
,再由直线方程和椭圆方程联立,利用根与系数关系求出两点P,Q的横坐标之和,代入上面的方程即可得到m与k的关系,由此可以求出m的取值范围.解答:解:(Ⅰ)由a2=2,b2=1,所以c2=a2-b2=1,所以c=1,则F1(-1,0),F2(1,0)
设M(x,y),则MF1的中点为
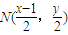 ,
,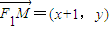 ,
,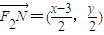 .
.∵MF1⊥NF2,∴
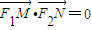 ,即
,即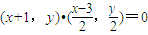 ,
,∴
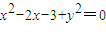 (1)
(1)又有
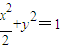 (2)
(2)由(1)、(2)解得
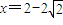 或
或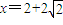 (舍去)
(舍去)所以点M 到y轴的距离为
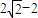 .
.(Ⅱ)设P(x1,y1)Q(x2,y2),
∵OPRQ为平行四边形,∴x1+x2=xR,y1+y2=yR.
∵R点在椭圆上,∴
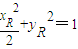 ,即
,即 ,
,即
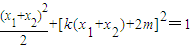 ,
,化简得,
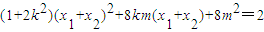 (3).
(3).由
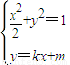 ,得(1+2k2)x2+4kmx+2m2-2=0.
,得(1+2k2)x2+4kmx+2m2-2=0.由△>0,得2k2+1>m2 (4),
且
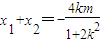 .
. 代入(3)式,得
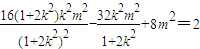 ,
,化简得4m2=1+2k2,代入(4)式,得m≠0.
又4m2=1+2k2≥1,解得
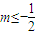 或
或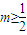 .
.点评:本题考查了直线与圆锥曲线的关系,考查了平面向量在解析几何中的应用,训练了整体代换思想,训练了学生的计算能力,特别是(Ⅱ)中的坐标转换是解决该题的关键所在.此题属于难题.

练习册系列答案
相关题目
 (2013•临沂二模)
(2013•临沂二模) 的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线
的左、右焦点分别为F1、F2,上顶点为A,△AF1F2为正三角形,且以线段F1F2为直径的圆与直线 相切.
相切. 的对称点,动点M满足
的对称点,动点M满足 . 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由.
. 问是否存在一个定点T,使得动点M到定点T的距离为定值?若存在,求出定点T的坐标及此定值;若不存在,请说明理由. 的左、右焦点分别为
的左、右焦点分别为 ,离心率为
,离心率为 ,点A是椭圆上任一点,
,点A是椭圆上任一点, 的周长为
的周长为 .
. 任作一动直线l交椭圆C于
任作一动直线l交椭圆C于 两点,记
两点,记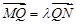 ,若在线段
,若在线段 上取一点R,使得
上取一点R,使得 ,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
,则当直线l转动时,点R在某一定直线上运动,求该定直线的方程.
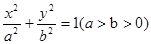 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为 ,
, ,离心率
,离心率 。
。 ,
, ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在直线
的交点在直线 上。
上。