题目内容
已知函数y=x-1,令x=―4,―3,―2,-1,0,1,2,3,4,可得函数图象上的九个点,在这九个点中随机取出两个点P1(x1,y1),P2(x2,y2),
(1)求P1,P2两点在双曲线xy=6上的概率;
(2)求P1,P2两点不在同一双曲线xy=k(k≠0)上的概率。
(1)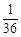 ;(2)
;(2) .
.
解析试题分析:(1)写出这9个点的坐标,计算从九个点中选2个点的选法数;从中找出满足方程xy=6的点的个数,计算从中选2个点的选法数,代人古典概型概率公式计算;
(2)两点在同一双曲线xy=k(k≠0)上的有(-3,-4)和(4,3);(-2,-3)和(3,2);(-1,-2)和(2,1)共3对,代人古典概型概率公式计算.
试题解析:(1)函数图象上的九个点分别是:(―4,―5),(―3,―4),(―2,―3),
(―1,―2),(0,―1),(1,0),(2,1),(3,2),(4,3) 2分
从九个点中选2个点共有36种,其中在双曲线xy=6上 4分
设有:(―2,―3),(3,2),故:P1=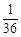 6分
6分
(2)P1,P2在同一双曲线xy=k(k≠0)的有(―3,―4)和(4,3);(―2,―3)和(3,2);
(―1,―2)和(2,1) 9分
故:P2=1-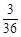 =
= 12分.
12分.
考点:古典概型及其概率计算公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t(单位:℃) | t≤22 | 22<t≤28 | 28<t≤32 | t>32 |
| 天数 | 6 | 12 | Y | Z |
某水果商根据多年的销售经验,六月份的日最高气温t(单位:℃)对西瓜的销售影响如下表:
| 日最高气温t(单位:℃) | t≤22 | 22<t≤28 | 28<t≤32 | t>32 |
| 日销售额X(单位:千元) | 2 | 5 | 6 | 8 |
(2)若视频率为概率,求六月份西瓜日销售额的期望和方差;
(3)在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
 .
.
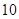 个同样型号的产品中,有
个同样型号的产品中,有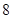 个是正品,
个是正品,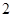 个是次品,从中任取
个是次品,从中任取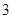 个,求(1)其中所含次品数
个,求(1)其中所含次品数 的期望、方差;(2)事件“含有次品”的概率。
的期望、方差;(2)事件“含有次品”的概率。