题目内容
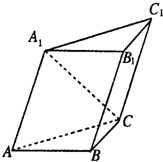 (2010•郑州三模)已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2
(2010•郑州三模)已知斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2| 3 |
(Ⅰ)求侧棱AA1与底面ABC所成角的大小;
(Ⅱ)求侧面A1ABB1与底面ABC所成二面角的正切值;
(Ⅲ)求侧棱B1B和侧面A1ACC1的距离.
分析:(1)确定∠A1AC为侧棱AA1与底面ABC所成的角,可得结论;
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1,可得∠A1NM即为所求二面角的平面角,从而可得结论;
(3)作BH⊥AC于点H,因为BB1∥侧面A1ACC1,所以点B到侧面A1ACC1的距离即为BB1到侧面A1ACC1的距离,利用等面积可求.
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1,可得∠A1NM即为所求二面角的平面角,从而可得结论;
(3)作BH⊥AC于点H,因为BB1∥侧面A1ACC1,所以点B到侧面A1ACC1的距离即为BB1到侧面A1ACC1的距离,利用等面积可求.
解答: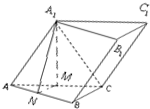 解:(1)因为侧面A1ACC1⊥底面ABC,AA1?侧面A1ACC1,
解:(1)因为侧面A1ACC1⊥底面ABC,AA1?侧面A1ACC1,
侧面A1ACC1∩底面ABC=AC
所以直线AA1在底面ABC内的射影为直线AC
故∠A1AC为侧棱AA1与底面ABC所成的角
又AC=AA1=A1C,所以∠A1AC=60°为所求. (4分)
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1
由(1)知A1M⊥AC
故A1M⊥底面ABC,A1M⊥AB
又MN∥BC,∠ABC=90°
所以MN⊥AB,又MN∩A1M=M,所以AB⊥平面A1MN
则∠A1NM即为所求二面角的平面角
在RtA1MN中,A1M=
AC=3,MN=
BC=1,∠A1MN=90°
所以tan∠A1MN=
=3,即所求二面角的正切值为3. (8分)
(3)作BH⊥AC于点H,因为BB1∥侧面A1ACC1
所以点B到侧面A1ACC1的距离即为BB1到侧面A1ACC1的距离.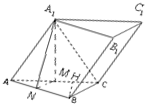
由(1)(2)知,BH的长即为所求
在Rt∠ABC中,BH=
=
所以侧棱B1B和侧面A1ACC1的距离为
. (12分)
 解:(1)因为侧面A1ACC1⊥底面ABC,AA1?侧面A1ACC1,
解:(1)因为侧面A1ACC1⊥底面ABC,AA1?侧面A1ACC1,侧面A1ACC1∩底面ABC=AC
所以直线AA1在底面ABC内的射影为直线AC
故∠A1AC为侧棱AA1与底面ABC所成的角
又AC=AA1=A1C,所以∠A1AC=60°为所求. (4分)
(2)取AC,AB的中点分别为M,N,连结A1M,MN,NA1
由(1)知A1M⊥AC
故A1M⊥底面ABC,A1M⊥AB
又MN∥BC,∠ABC=90°
所以MN⊥AB,又MN∩A1M=M,所以AB⊥平面A1MN
则∠A1NM即为所求二面角的平面角
在RtA1MN中,A1M=
| ||
| 2 |
| 1 |
| 2 |
所以tan∠A1MN=
| A1M |
| MN |
(3)作BH⊥AC于点H,因为BB1∥侧面A1ACC1
所以点B到侧面A1ACC1的距离即为BB1到侧面A1ACC1的距离.

由(1)(2)知,BH的长即为所求
在Rt∠ABC中,BH=
| AB•BC |
| AC |
2
| ||
| 3 |
所以侧棱B1B和侧面A1ACC1的距离为
2
| ||
| 3 |
点评:本题考查空间角,考查线面距离,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目