题目内容
8.在平面直角坐标系中,直线x-2y+1=0被圆(x-2)2+(y+1)2=9截得的弦长为4.分析 求出已知圆的圆心为C,半径r.利用点到直线的距离公式,算出点C到直线直线l的距离d,由垂径定理加以计算,可得直线x-2y+1=0被圆截得的弦长.
解答 解:圆(x-2)2+(y+1)2=9的圆心为C(2,-1),半径r=3,
∵点C到直线直线x-2y+1=0的距离d=$\frac{|2+2+1|}{\sqrt{1+4}}$=$\sqrt{5}$,
∴根据垂径定理,得直线x-2y+1=0被圆(x-2)2+(y+1)2=9截得的弦长为2$\sqrt{{r}^{2}-{d}^{2}}$=2×2=4
故答案为:4.
点评 本题给出直线与圆的方程,求直线被圆截得的弦长,着重考查点到直线的距离公式、圆的方程和直线与圆的位置关系等知识,属于基础题.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
 把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求:
把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:2,母线长10cm.圆台侧面展开是一个$\frac{1}{4}$圆环,求: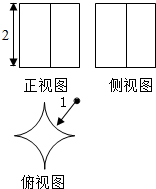 已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.
已知某几何体的三视图如图所示,其中俯视图是一个边长为2的正方形切去了四个以顶点为圆心1为半径的四分之一圆,则该几何体的表面积为8+2π.