题目内容
已知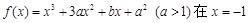 时的极值为0.
时的极值为0.
(1)求常数a,b的值;
(2)求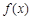 的单调区间.
的单调区间.
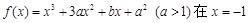 时的极值为0.
时的极值为0.(1)求常数a,b的值;
(2)求
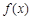 的单调区间.
的单调区间. (1) a = 2,b = 9.
(2) 由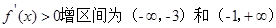 ;
;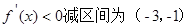
(2) 由
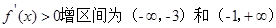 ;
;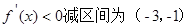
本试题主要是考查了导数在研究函数中的运用。利用导数的符号与函数单调性的关系求解参数的值和单调区间。
(1)利用函数式求解导数,然后分析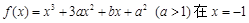 时的极值为0.,说明在x=-1处的导数值为0,那么可得a,b的值。
时的极值为0.,说明在x=-1处的导数值为0,那么可得a,b的值。
(2)因为f (x) = x3 + 6 x 2 + 9 x + 4,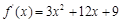
因此解二次不等式得到不等式大于零或者小于零的解集,即为单调区间。
解:(1) 由题易知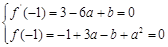
解得a = 2,b = 9. 6分
(2) f (x) = x3 + 6 x 2 + 9 x + 4,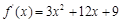
由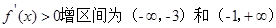
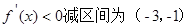 13分
13分
(1)利用函数式求解导数,然后分析
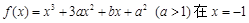 时的极值为0.,说明在x=-1处的导数值为0,那么可得a,b的值。
时的极值为0.,说明在x=-1处的导数值为0,那么可得a,b的值。(2)因为f (x) = x3 + 6 x 2 + 9 x + 4,
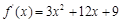
因此解二次不等式得到不等式大于零或者小于零的解集,即为单调区间。
解:(1) 由题易知
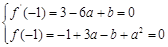
解得a = 2,b = 9. 6分
(2) f (x) = x3 + 6 x 2 + 9 x + 4,
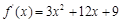
由
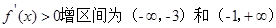
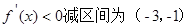 13分
13分
练习册系列答案
相关题目
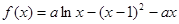 (常数
(常数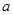
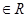 ).
).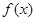 的单调区间;(5分)
的单调区间;(5分)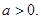 如果对于
如果对于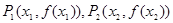
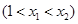 ,存在
,存在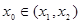 ,使得
,使得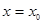 处的切线
处的切线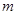 ∥
∥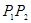 ,求证:
,求证: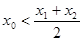 .(7分)
.(7分)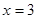 是函数
是函数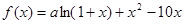 的一个极值点。
的一个极值点。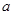 ; (2)求函数
; (2)求函数 的单调区间;
的单调区间;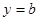 与函数
与函数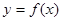 的图象有3个交点,求
的图象有3个交点,求 的取值范围。
的取值范围。 ,定义
,定义 是
是 的导函数
的导函数 的导函数,若方程
的导函数,若方程 有实数解
有实数解 ,则称点
,则称点 为函数
为函数 对称:
对称: 有实数解
有实数解 ,则,
,则,
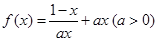 .
.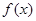 在
在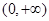 的单调性并证明;
的单调性并证明;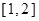 上的最小值。
上的最小值。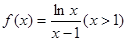
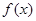 的单调性;
的单调性;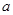 、使得关于
、使得关于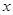 的不等式
的不等式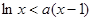 在(1,
在(1,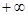 )上恒成立,若存在,求出
)上恒成立,若存在,求出 (a≠0)
(a≠0) ,e]的最大值;
,e]的最大值;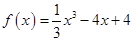 .
.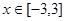 ,试求函数在此区间上的最大值与最小值.
,试求函数在此区间上的最大值与最小值.