题目内容
【题目】已知函数f(x)=m﹣|2x+1|﹣|2x﹣3|,若x0∈R,不等式f(x0)≥0成立,
(1)求实数m的取值范围;
(2)若x+2y﹣m=6,是否存在x,y,使得x2+y2=19成立,若存在,求出x,y值,若不存在,请说明理由.
【答案】
(1)解:由题意可得函数f(x)=m﹣|2x+1|﹣|2x﹣3|≥0有解,即 m≥|2x+1|+|2x﹣3|有解,
故 m大于或等于|2x+1|+|2x﹣3|的最小值.
由于|2x+1|+|2x﹣3|≥|(2x+1)﹣(2x﹣3)|=4,∴m≥4
(2)解:若x+2y﹣m=6,设存在x,y,使得x2+y2=19成立,则圆x2+y2=19和直线x+2y﹣m=6有交点,
即圆心(0,0)到直线x+2y﹣m﹣6=0的距离小于或等于半径 ![]() ,
,
即 ![]() ≤
≤ ![]() ,故当﹣6﹣
,故当﹣6﹣ ![]() ≤m≤﹣6+
≤m≤﹣6+ ![]() 时,圆x2+y2=19和直线x+2y﹣m=6有交点.
时,圆x2+y2=19和直线x+2y﹣m=6有交点.
由 ![]() ,求得
,求得 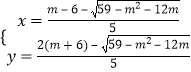 ,或
,或 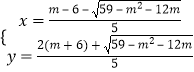
【解析】(1)由题意可得m≥|2x+1|+|2x﹣3|有解,利用绝对值三角不等式求得|2x+1|+|2x﹣3|的最小值,可得m的范围.(2)要使存在x,y,只要圆x2+y2=19和直线x+2y﹣m=6有交点,即圆心(0,0)到直线x+2y﹣m﹣6=0的距离小于或等于半径 ![]() ,由此求得m的范围.再解圆x2+y2=19和直线x+2y﹣m=6组成的方程组,求得直线和圆交点的坐标,即为所求的x、y的值.
,由此求得m的范围.再解圆x2+y2=19和直线x+2y﹣m=6组成的方程组,求得直线和圆交点的坐标,即为所求的x、y的值.
【考点精析】根据题目的已知条件,利用绝对值不等式的解法的相关知识可以得到问题的答案,需要掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

 名校课堂系列答案
名校课堂系列答案【题目】户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,对本单位的50名员工进行了问卷调查,得到了如下列联表:
喜欢户外运动 | 不喜欢户外运动 | 合计 | |
男性 | 5 | ||
女性 | 10 | ||
合计 | 50 |
已知在这50人中随机抽取1人抽到喜欢户外运动的员工的概率是 ![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜欢户外运动与性别有关?并说明你的理由;
(3)经进一步调查发现,在喜欢户外运动的10名女性员工中,有4人还喜欢瑜伽.若从喜欢户外运动的10位女性员工中任选3人,记ξ表示抽到喜欢瑜伽的人数,求ξ的分布列和数学期望.
下面的临界值表仅供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
