Question

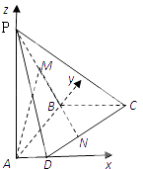
【题目】如图，在四棱锥P﹣ABCD中，侧棱PA⊥底面ABCD，AD∥BC，∠ABC=90°，PA=AB=BC=2，AD=1，M是棱PB的中点．

（1）求证：AM∥平面PCD；
（2）设点N是线段CD上的一动点，当点N在何处时，直线MN与平面PAB所成的角最大？并求出最大角的正弦值．

Answer 1

【答案】
（1）证明：以A为坐标原点，建立如图所示的空间直角坐标系，则A（0，0，0），B（0，2，0），C（2，2，0），D（1，0，0），P（0，0，2），M（0，1，1）

设平面PCD的法向量是

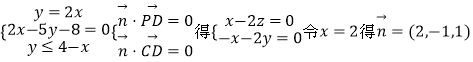
又

（2）解：由点N是线段CD上的一点，可设

；

；

平面PAB的一个法向量为

设MN与平面PAB成θ角，则

令1+λ=t∈[1，2]

当

∴当点N是线段CD上靠近点C的三等分点时，MN与平面PAB所成角最大，最大角的正弦值为

【解析】（1）以点A为原点建立如图所示的空间直角坐标系，求出 的坐标，再求出平面平面PCD的一个法向量 ，由 =0且AM面PCD内得答案；（2）利用空间向量求出使直线MN与平面PAB所成的角最大时N的位置，然后再求出平面PBN的一个法向量，而 是平面PAB的一个法向量，由两个法向量所成角的余弦值求得结论．
【考点精析】通过灵活运用直线与平面平行的判定和空间角的异面直线所成的角，掌握平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行；简记为：线线平行，则线面平行；已知为两异面直线，A，C与B，D分别是上的任意两点，所成的角为，则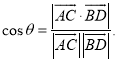即可以解答此题．