题目内容
【题目】已知椭圆C的两个焦点分别为
，且椭圆C过点P（3，2）．
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）与直线OP平行的直线交椭圆C于A，B两点，求△PAB面积的最大值．
【答案】（1） 
；（2） 6
【解析】
试题分析：（Ⅰ）由题意设椭圆方程为
，利用椭圆定义求得
，结合隐含条件求得
，则椭圆方程可求；（Ⅱ）求出
，设与直线
平行的直线方程为
联立直线和椭圆方程，运用韦达定理和判别式大于
，以及弦长公式，点到直线的距离公式和三角形的面积公式，结合基本不等式即可得到所求最大值．
试题解析：解：（Ⅰ）设椭圆
的方程为，
由题意可得
解得
，
故椭圆
的方程为．
（Ⅱ）直线
方程为
，设直线
方程为
将直线
的方程代入椭圆
的方程并整理得
设
．
当
，即
时，
有
所以
到直线
的距离
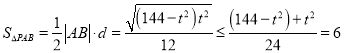
面积的最大值为6
一诺书业暑假作业快乐假期云南美术出版社系列答案
【题目】某初级中学有三个年级，各年级男、女人数如下表：
初一年级 | 初二年级 | 初三年级 | |
女生 | 370 |
| 200 |
男生 | 380 | 370 | 300 |
已知在全校学生中随机抽取1名，抽到初二年级女生的概率是0.19.
（1）求
的值；
（2）用分层抽样的方法在初三年级中抽取一个容量为5的样本，求该样本中女生的人数；
（3）用随机抽样的方法从初二年级女生中选出8人，测量它们的左眼视力，结果如下：1.2，1.5，1.2，1.5，1.5，1.3，1.0，1.2．把这8人的左眼视力看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.1的概率．
【题目】某商店计划每天购进某商品若干件,商店每销售1件该商品可获利50元.若供大于求，剩余商品全部退回，则每件商品亏损10元；若供不应求，则从外部调剂，此时每件调剂商品可获利30元.
（Ⅰ）若商店一天购进该商品10件,求当天的利润y（单位:元）关于当天需求量n（单位:件,n∈N）的函数解析式；
（Ⅱ）商店记录了50天该商品的日需求量（单位:件）,整理得下表:
日需求量n | 8 | 9 | 10 | 11 | 12 |
频数 | 10 | 10 | 15 | 10 | 5 |
①假设该店在这50天内每天购进10件该商品,求这50天的日利润（单位:元）的平均数；
②若该店一天购进10件该商品,记“当天的利润在区间
”为事件A，求P（A）的估计值.
