题目内容
20.已知函数f(x)=ax3+bx2+c,其导函数f′(x)的图象如图,则函数f(x)的极小值为( )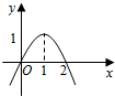
| A. | c | B. | a+b+c | C. | 8a+4b+c | D. | 3a+2b |
分析 根据导函数的图象,确定函数的单调性,从而可得函数f(x)的极小值.
解答 解:f′(x)=3ax2+2bx,根据导函数的图象,
可知0,2是方程3ax2+2bx=0的根,
当x<0或x>2时,f′(x)<0,函数为减函数,
当0<x<2时,f′(x)>0,函数为增函数,
∴x=0时,函数f(x)取得极小值,极小值为f(0)=c,
故选:A.
点评 本题考查导函数的图象,考查极值的计算,属于基础题.

练习册系列答案
相关题目
8.设函数f(x)=x2+4x-1.
(1)若对一切实数x,f(x)+(m-1)x2-(4+m)x<0恒成立,求m的取值范围;
(2)若对于任意x∈[-1,2],f(x)<-m+5恒成立,求m的取值范围.
(1)若对一切实数x,f(x)+(m-1)x2-(4+m)x<0恒成立,求m的取值范围;
(2)若对于任意x∈[-1,2],f(x)<-m+5恒成立,求m的取值范围.
15.若sinα=$\frac{1}{5}$,且α是第二象限角,则$\frac{sin2α+si{n}^{2}α}{co{s}^{2}α}$ 的值为( )
| A. | $\frac{\sqrt{6}}{4}$ | B. | -$\frac{\sqrt{6}}{4}$ | C. | $\frac{\sqrt{6}}{6}$+$\frac{1}{24}$ | D. | -$\frac{\sqrt{6}}{6}+\frac{′1}{24}$ |
10.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,3,4},则∁U(A∩B)为( )
| A. | {1,2,4} | B. | {0,1,4} | C. | {0,2,4} | D. | {0,2,3,4} |