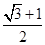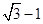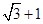题目内容
已知椭圆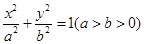 与双曲线
与双曲线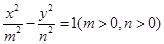 有相同的焦点
有相同的焦点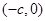 和
和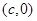 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
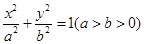 与双曲线
与双曲线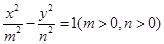 有相同的焦点
有相同的焦点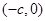 和
和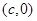 ,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为
,若c是a与m的等比中项,n2是2m2与c2的等差中项,则椭圆的离心率为A.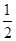 | B.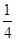 | C.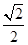 | D.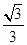 |
A
试题分析:根据是a、m的等比中项可得c2=am,根据椭圆与双曲线有相同的焦点可得a2+b2=m2+n2=c,根据n2是2m2与c2的等差中项可得2n2=2m2+c2,联立方程即可求得a和c的关系,进而求得离心率e.
解:根据题意,
 ,故选A.
,故选A.点评:本题主要考查了椭圆的性质,属基础题.

练习册系列答案
相关题目
 过定点
过定点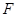
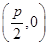 ,且与直线
,且与直线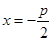 相切,其中
相切,其中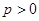 .设圆心
.设圆心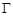 的程为
的程为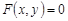
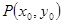 (
(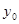
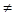 0) ,方向向量
0) ,方向向量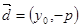 的直线
的直线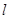 (不过P点)与曲线
(不过P点)与曲线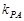 ,
,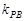 ,计算
,计算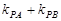 ;
;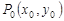 、
、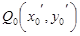 ,分别过点
,分别过点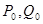 作倾斜角互补的两条直线
作倾斜角互补的两条直线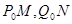 分别与曲线
分别与曲线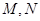 两点,求证直线
两点,求证直线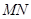 的斜率为定值;
的斜率为定值;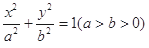 .
.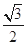 ,求椭圆的标准方程;
,求椭圆的标准方程;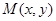 与两个定点
与两个定点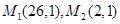 的距离之比等于5.
的距离之比等于5.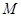 的轨迹方程,并说明轨迹是什么图形;
的轨迹方程,并说明轨迹是什么图形;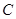 ,过点
,过点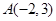 的直线
的直线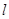 被
被 中,已知△ABC顶点
中,已知△ABC顶点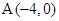 和
和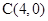 ,顶点B在椭圆
,顶点B在椭圆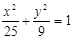 上,则
上,则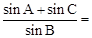 .
. 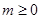 ,在平面直角坐标系中,已知向量
,在平面直角坐标系中,已知向量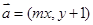 ,向量
,向量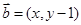 ,
,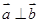 ,动点
,动点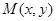 的轨迹为E.
的轨迹为E.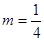 ,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且
,证明:存在圆心在原点的圆,使得该圆的任意一条切线与轨迹E恒有两个交点A,B,且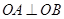 (O为坐标原点),并求出该圆的方程;
(O为坐标原点),并求出该圆的方程;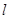 与圆C:
与圆C: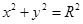 (1<R<2)相切于A1,且
(1<R<2)相切于A1,且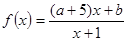 在
在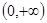 上是增函数;命题q:方程
上是增函数;命题q:方程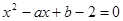 有两个不相等的负实数根。求使得p
有两个不相等的负实数根。求使得p q是真命题的实数对
q是真命题的实数对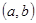 为坐标的点的轨迹图形及其面积。
为坐标的点的轨迹图形及其面积。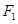 和
和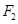 分别是双曲线
分别是双曲线 (
(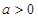 ,
, )的两个焦点,
)的两个焦点,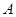 和
和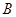 是以
是以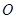 为圆心,以
为圆心,以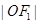 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且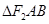 是等边三角形,则该双曲线的离心率为( )
是等边三角形,则该双曲线的离心率为( )