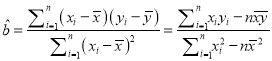Question

【题目】为响应新农村建设，某村计划对现有旧水渠进行改造，已知旧水渠的横断面是一段抛物线弧，顶点为水渠最底端（如图），渠宽为4m，渠深为2m．

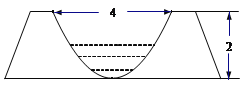
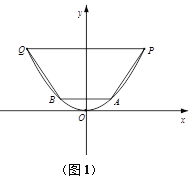
（1）考虑到农村耕地面积的减少，为节约水资源，要减少水渠的过水量，在原水渠内填土，使其成为横断面为等腰梯形的新水渠（如图（1）建立平面直角坐标系），新水渠底面与地面平行（不改变渠宽），问新水渠底宽为多少时，所填土的土方量最少？

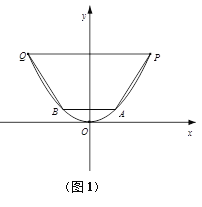
（2）考虑到新建果园的灌溉需求，要增大水渠的过水量，现把旧水渠改挖（不能填土）成横断面为等腰梯形的新水渠（如图（2）建立平面直角坐标系），使水渠的底面与地面平行（不改变渠深），要使所挖土的土方量最少，请你设计水渠改挖后的底宽，并求出这个底宽．

Answer 1

【答案】（1）；（2）改挖后的水渠的底宽为时，可使挖土的土方量最少

【解析】试题分析：（1）建立坐标系，设拋物线的方程为,由已知点在抛物线上，推导出拋物线的方程，可得梯形面积，利用导数可得结论；(2)为了使挖掉的土最少,等腰梯形的两腰必须与拋物线相切,设切点，则函数在点的切线方程为,由此能推导出设计改挖后的水渠的底宽为时，可使用权所挖土的土方星最少.

试题解析：建立如图所示的直角坐标系，

设抛物线的方程为，由已知点在抛物线上，得，所以抛物线的方程为.

（1）为了使填入的土最少，内接等腰梯形的面积要最大，如图1，设点，则此时梯形APQB的面积，

∴,令，得，

当时， ， 单调递增，当时， ， 单调递减，

所以当时， 有最大值，改挖后的水渠的底宽为m时，可使填土的土方量最少.

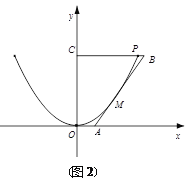
（2）为了使挖掉的土最少，等腰梯形的两腰必须与抛物线相切，如图2，设切点，则函数在点M处的切线方程为，分别令得，所以此时梯形OABC的面积，当且仅当时，等号成立，此时.所以设计改挖后的水渠的底宽为m时，可使挖土的土方量最少.