题目内容
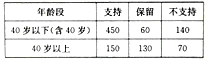
【题目】为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天100颗种子浸泡后的发芽率,得到如下表格:

(1)从这5天中任选2天,记发芽的种子数分别为![]() ,求事件“
,求事件“![]() 均不小于25” 的概率;
均不小于25” 的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得到的线性回归方程是否可靠?
参考公式: 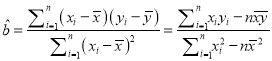 ,
, ![]() .
.
【答案】(1) ![]() .(2)
.(2) ![]() =
=![]() x-3. (3)是可靠的.
x-3. (3)是可靠的.
【解析】试题分析:
(1)结合题意列出所有可能的事件,利用古典概型公式可得:事件“![]() 均不小于25” 的概率是
均不小于25” 的概率是![]() ;
;
(2)首先求得样本中心点为![]() ,结合线性回归方程系数计算公式可得回归方程为
,结合线性回归方程系数计算公式可得回归方程为![]() ;
;
(3)结合回归方程的预测作用计算可得(2)中所得到的线性回归方程是可靠的.
试题解析:
(1)所有的基本事件为
(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),
(30,26),(30,16),(26,16),共10个.
设“m,n均不小于25”为事件A,则事件A包含的基本事件为
(25,30),(25,26),(30,26),共3个.
所以P(A)=![]() .
.
(2)由数据得,另3天的平均数![]() ,
, ![]() ,
,
法一: 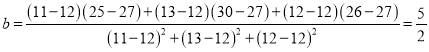 ,
,
法二: ![]() ,
,
所以![]() =27-
=27-![]() ×12=-3,
×12=-3,
所以y关于x的线性回归方程为![]() =
=![]() x-3.
x-3.
(3)依题意得,当x=10时,=22,|22-23|<2;当x=8时,=17,|17-16|<2,
所以(2)中所得到的线性回归方程是可靠的.

【题目】随着我国经济的快速发展,民用汽车的保有量也迅速增长.机动车保有量的发展影响到环境质量、交通安全、道路建设等诸多方面.在我国,尤其是大中型城市,机动车已成为城市空气污染的重要来源.因此,合理预测机动车保有量是未来进行机动车污染防治规划、道路发展规划等的重要前提.从2012年到2016年,根据“云南省某市国民经济和社会发展统计公报”中公布的数据,该市机动车保有量数据如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
机动车保有量 | 169 | 181 | 196 | 215 | 230 |
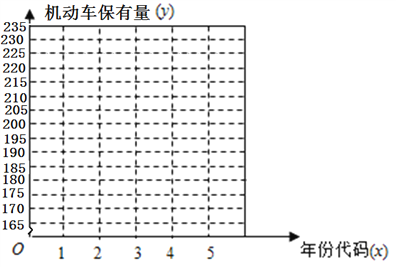
(1)在图所给的坐标系中作出数据对应的散点图;
(2)建立机动车保有量![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017年该市机动车保有量.
附注:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
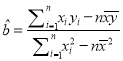 ,
, ![]() .
.