题目内容
某车间共有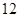
名工人,随机抽取
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 
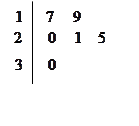
(Ⅰ) 根据茎叶图计算样本均值;
(Ⅱ) 日加工零件个数大于样本均值的工人为优秀工人,根据茎叶图推断该车间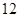名工人中有几名优秀工人;
(Ⅲ) 从该车间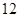名工人中,任取
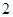人,求恰有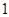
名优秀工人的概率.
（1）22
（2）4
（3）10:33
解析试题分析：解:(1)由题意可知,样本均值
3分
(2)
样本6名个人中日加工零件个数大于样本均值的工人共有2名, 
可以推断该车间12名工人中优秀工人的人数为:
7分
(3)从该车间12名工人中,任取2人有
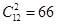种方法,
而恰有1名优秀工人有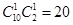
所求的概率为:
12分
考点：古典概型
点评：主要是考查了古典概型概率的运用，属于基础题。
练习册系列答案
相关题目
某超市为了解顾客的购物量及结算时间等信息，安排一名员工随机收集了在该超市购物的50位顾客的相关数据，如下表所示：
一次购物量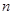 （件） | 1≤n≤3 | 4≤n≤6 | 7≤n≤9 | 10≤n≤12 | n≥13 |
| 顾客数（人） |  | 20 | 10 | 5 |  |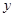
| 结算时间（分钟/人） | 0.5 | 1 | 1.5 | 2 | 2.5 |
（1）确定
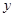与的值；（2）若将频率视为概率，求顾客一次购物的结算时间
的分布列与数学期望；（3）在（2）的条件下，若某顾客到达收银台时前面恰有2位顾客需结算，且各顾客的结算相互独立，求该顾客结算前的等候时间不超过2分钟的概率.
某高校在2013年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩共分五组，得到频率分布表如下表所示。
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [160,165) | 5 | 0.05 |
| 第二组 | [165,170) | 35 | 0.35 |
| 第三组 | [170,175) | 30 | a |
| 第四组 | [175,180) | b | 0.2 |
| 第五组 | [180,185) | 10 | 0.1 |
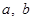的值； （Ⅱ）为了能选出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样的方法抽取12人进入第二轮面试，求第3、4、5组中每组各抽取多少人进入第二轮的面试；考生李翔的笔试成绩为178分，但不幸没入选这100人中，那这样的筛选方法对该生而言公平吗？为什么？
（Ⅲ）在（2）的前提下，学校决定在12人中随机抽取3人接受“王教授”的面试，设第4组中被抽取参加“王教授”面试的人数为
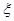，求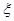的分布列和数学期望． 为了整顿道路交通秩序，某地考虑将对行人闯红灯进行处罚．为了了解市民的态度，在普通行人中随机选取了200人进行调查，得到如下数据：
| 处罚金额x(元) | 0 | 5 | 10 | 15 | 20 |
| 会闯红灯的人数y | 80 | 50 | 40 | 20 | 10 |
(Ⅰ)求这两种金额之和不低于20元的概率；
(Ⅱ)若用X表示这两种金额之和，求X的分布列和数学期望．
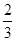，且每次射击的结果互不影响
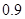倍、
倍、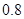
倍的概率分别为
、
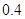；第二年可以使出口额为第一年的
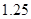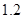倍、
、
倍、
、
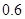。实施每种方案第一年与第二年相互独立。令
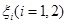表示方案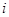
实施两年后出口额达到危机前的倍数。
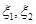的分布列；
万元、
万元、
万元，问实施哪种方案的平均利润更大？
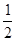，乙投篮一次命中的概率为
．每人各投4个球，两人投篮命中的概率互不影响．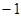
分，求乙所得分数
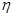的概率分布和数学期望．
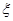，求
，求