题目内容
因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施。若实施方案一,预计第一年可以使出口额恢复到危机前的 倍、
倍、 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 、
、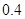 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的 倍、
倍、 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 、
、 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的 倍、
倍、 倍的概率分别为
倍的概率分别为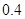 、
、 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令 表示方案
表示方案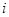 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。
(1)写出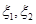 的分布列;
的分布列;
(2)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(3)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为 万元、
万元、 万元、
万元、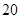 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大?
(1)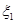 ,
,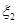 的分布列为:
的分布列为: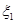
1.25 1.125 1 0.9 0.8 P 0.15 0.15 0.35 0.15 0.2
(2)实施方案二的概率更大
1.44 1.2 1 0.96 0.8 P 0.08 0.24 0.18 0.2 0.3
(3)第一个方案的平均利润更大
解析试题分析:(1) 根据题意,由于实施方案一,预计第一年可以使出口额恢复到危机前的 某小组共有 通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表: 某商场经销某商品,根据以往资料统计,顾客采用的付款期数 倍、
倍、 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 、
、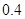 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的 倍、
倍、 倍、
倍、 倍的概率分别为
倍的概率分别为 、
、 、
、 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的 倍、
倍、 倍的概率分别为
倍的概率分别为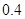 、
、 ,那么可知
,那么可知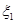 ,
,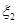 的分布列为:
的分布列为: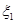
1.25 1.125 1 0.9 0.8 P 0.15 0.15 0.35 0.15 0.2 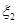
1.44 1.2 1 0.96 0.8 P 0.08 0.24 
天府数学系列答案
天府前沿系列答案
文科爱好者系列答案
理科爱好者系列答案
新学案同步导与练系列答案
名师大课堂系列答案
351高效课堂导学案系列答案
状元成才路状元导练系列答案

探究乐园高效课堂系列答案
 五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
五位同学,他们的身高(单位:米)以及体重指标(单位:千克/米2)如下表所示:
(1)从该小组身高低于1.80的同学中任选2人,求选到的2人身高都在1.78以下的概率;
A
B
C
D
E
身高
1.69
1.73
1.75
1.79
1.82
体重指标
19.2
25.1
18.5
23.3
20.9
(2)从该小组同学中任选2人,求选到的2人的身高都在1.70以上且体重指标都在[18.5,23.9)中的概率.
性别与看营养说明列联表 单位: 名
(1)从这50名女生中按是否看营养说明采取分层抽样,抽取一个容量为10的样本,问样本中看与不看营养说明的女生各有多少名?
男
女
总计
看营养说明
50
30
80
不看营养说明
10
20
30
总计
60
50
110
(2)根据以上列联表,能否在犯错误的概率不超过0.01的前提下认为性别与是否看营养说明之间有关系?
下面的临界值表供参考:
(参考公式:
0.15
0.10
0.05
0.025
0.010
0.005
0.001

2.072
2.706
3.841
5.024
6.635
7.879
10.828
 ,其中
,其中 )
)
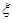 的分布列为
的分布列为
商场经销一件该商品,采用1期付款,其利润为200元;分2期或3期付款,其利润为250元;分4期或5期付款,其利润为300元.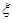
1
2
3
4
5

0.4
0.2
0.2
0.1
0.1
 表示经销一件该商品的利润.
表示经销一件该商品的利润.
(Ⅰ)求事件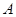 :“购买该商品的3位顾客中,至少有1位采用1期付款”的概率
:“购买该商品的3位顾客中,至少有1位采用1期付款”的概率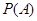 ;
;
(Ⅱ)求 的分布列及期望
的分布列及期望 与方差D
与方差D
 为取得红球的个数.
为取得红球的个数. 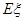 .
. 名工人,随机抽取
名工人,随机抽取 名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数. 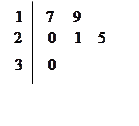
 人,求恰有
人,求恰有 名优秀工人的概率.
名优秀工人的概率.  小时收费
小时收费 元,超过
元,超过 元(不足
元(不足 小时.
小时. 小时的概率为
小时的概率为 ,停车付费多于
,停车付费多于 元的概率为
元的概率为 ,求甲停车付费恰为
,求甲停车付费恰为 元的概率.
元的概率.