题目内容
设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽取一个,并且取出不再放回,若以ξ和 分别表示取出次品和正品的个数.
分别表示取出次品和正品的个数.
(1)求 的概率分布、期望值及方差;
的概率分布、期望值及方差;
(2)求 的概率分布、期望值及方差.
的概率分布、期望值及方差.
 分别表示取出次品和正品的个数.
分别表示取出次品和正品的个数.(1)求
 的概率分布、期望值及方差;
的概率分布、期望值及方差;(2)求
 的概率分布、期望值及方差.
的概率分布、期望值及方差.(1)E( )=0×
)=0×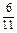 +1×
+1×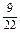 +2×
+2× =
= .V(
.V( )=(0-
)=(0- )2×
)2×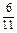 +
+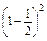 ×
×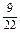 +
+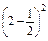 ×
× =
=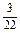 +
+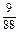 +
+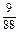 =
=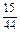 .
.
(2)E( )=E(3-
)=E(3- )=3-E(
)=3-E( )=3-
)=3- =
=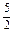 .V(
.V( )=(-1)2V(
)=(-1)2V( )=
)=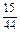 .
.
 )=0×
)=0×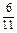 +1×
+1×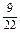 +2×
+2× =
= .V(
.V( )=(0-
)=(0- )2×
)2×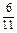 +
+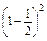 ×
×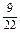 +
+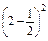 ×
× =
=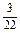 +
+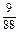 +
+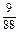 =
=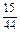 .
.(2)E(
 )=E(3-
)=E(3- )=3-E(
)=3-E( )=3-
)=3- =
=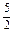 .V(
.V( )=(-1)2V(
)=(-1)2V( )=
)=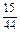 .
.(1) 的可能值为0,1,2.
的可能值为0,1,2.
若 =0,表示没有取出次品,其概率为:
=0,表示没有取出次品,其概率为:
P( =0)=
=0)=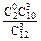 =
=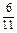 ;
;
同理,有P( =1)=
=1)=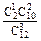 =
=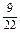 ;P(
;P( =2)=
=2)=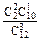 =
= .
.
∴ 的概率分布为:
的概率分布为:
∴E( )=0×
)=0×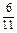 +1×
+1×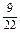 +2×
+2× =
= .
.
V( )=(0-
)=(0- )2×
)2×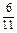 +
+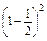 ×
×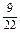 +
+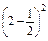 ×
×
=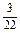 +
+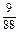 +
+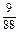 =
=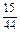 .
.
(2) 的可能值为1,2,3,显然
的可能值为1,2,3,显然 +
+ =3.
=3.
P( =1)=P(
=1)=P( =2)=
=2)= ,P(
,P( =2)=P(
=2)=P( =1)=
=1)=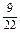 ,
,
P( =3)=P(
=3)=P( =0)=
=0)=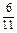 .
.
∴ 的概率分布为:
的概率分布为:
E( )=E(3-
)=E(3- )=3-E(
)=3-E( )=3-
)=3- =
=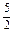 .
.
∵ =-
=- +3,∴V(
+3,∴V( )=(-1)2V(
)=(-1)2V( )=
)=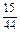 .
.
 的可能值为0,1,2.
的可能值为0,1,2.若
 =0,表示没有取出次品,其概率为:
=0,表示没有取出次品,其概率为:P(
 =0)=
=0)=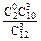 =
=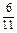 ;
;同理,有P(
 =1)=
=1)=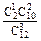 =
=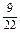 ;P(
;P( =2)=
=2)=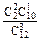 =
= .
.∴
 的概率分布为:
的概率分布为: | 0 | 1 | 2 |
| P | 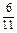 | 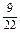 |  |
 )=0×
)=0×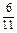 +1×
+1×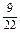 +2×
+2× =
= .
.V(
 )=(0-
)=(0- )2×
)2×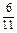 +
+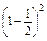 ×
×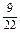 +
+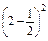 ×
×
=
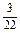 +
+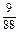 +
+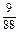 =
=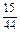 .
.(2)
 的可能值为1,2,3,显然
的可能值为1,2,3,显然 +
+ =3.
=3.P(
 =1)=P(
=1)=P( =2)=
=2)= ,P(
,P( =2)=P(
=2)=P( =1)=
=1)=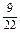 ,
,P(
 =3)=P(
=3)=P( =0)=
=0)=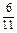 .
.∴
 的概率分布为:
的概率分布为:  | 1 | 2 | 3 |
| P |  | 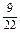 | 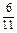 |
 )=E(3-
)=E(3- )=3-E(
)=3-E( )=3-
)=3- =
=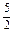 .
.∵
 =-
=- +3,∴V(
+3,∴V( )=(-1)2V(
)=(-1)2V( )=
)=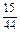 .
.
练习册系列答案
 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案
相关题目
 时刻一质点在数轴的原点,该质点
时刻一质点在数轴的原点,该质点 每经过
每经过 秒就要向右跳动一个单位长度,已知每次跳动,该质点向左的概率为
秒就要向右跳动一个单位长度,已知每次跳动,该质点向左的概率为 ,向右的概率为
,向右的概率为 .
. 秒时刻,该质点在数轴上
秒时刻,该质点在数轴上 处的概率.
处的概率. 处,求
处,求 、
、
 .
. ,求随机变量
,求随机变量 0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。
0~6:00定为职工活动时间,并成立了行政和教师两支篮球队,但由于工作性质所限,每月(假设为4周)每支球队只能组织两次活动,且两支球队的活动时间是相互独立的。 支球队每月两次都在同一时间活动的频率;
支球队每月两次都在同一时间活动的频率; ,求随机变量
,求随机变量 环的概率为
环的概率为 ,乙射击一次命中
,乙射击一次命中 ,若他们独立的射击两次,设乙命中
,若他们独立的射击两次,设乙命中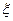 ,则
,则 ,
, 为甲与乙命中
为甲与乙命中 ;乙抛掷3次,记正面朝上的次为
;乙抛掷3次,记正面朝上的次为 .(Ⅰ)分别求
.(Ⅰ)分别求 的概
的概 率分布为右表所示,则
率分布为右表所示,则 的值为 。
的值为 。