题目内容
已知数列{an}满足a1=1,an+1=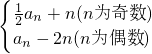 且bn=a2n-2(n∈N*)
且bn=a2n-2(n∈N*)
(1)求a2,a3,a4;
(2)求证:数列{bn}是等比数列,并求其通项公式;
(3)若Cn=-nbn,Sn为为数列{Cn}的前n项和,求Sn-2.
(1)解:a2= ,a3=-
,a3=- ,a4=
,a4= ;
;
(2)证明:
= =
= ,
,
又b1=a2-2=- ∴数列{bn}是公比为
∴数列{bn}是公比为 的等比数列
的等比数列
bn=(- )•
)• =-
=-
(3)由(2)知cn=n
Sn= +2×
+2× +3×
+3× +…+n
+…+n ①
①
 Sn=
Sn= +2×
+2× +…+(n-1)
+…+(n-1) +n
+n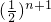 ②
②
①-②得: Sn=
Sn= +
+ +
+ +…+
+…+ -n
-n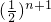
=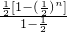 -n•
-n• =1-
=1- -
-
∴Sn=2-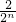 -
- =2-
=2-
∴Sn-2=-
分析:(1)分别将n=1,2,3,4代入到an+1=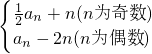 中即可得到a2,a3,a4的值.
中即可得到a2,a3,a4的值.
(2)根据bn=a2n-2,然后进行整理即可得到bn+1= bn,从而证明数列{bn}是等比数列,进而可求出数列{bn}的通项公式.
bn,从而证明数列{bn}是等比数列,进而可求出数列{bn}的通项公式.
(3)先根据(2)中{bn}的通项公式求出 Cn=-nbn,利用错位相减法求得数列{Cn}的前n项和,进而求得Sn-2.
点评:此题考查了有数列的递推关系求前4项的数值,等比数列的定义及通项公式,错位相减法求数列的前n项和,考查运算能力,属中档题.
 ,a3=-
,a3=- ,a4=
,a4= ;
;(2)证明:

=
 =
= ,
,又b1=a2-2=-
 ∴数列{bn}是公比为
∴数列{bn}是公比为 的等比数列
的等比数列bn=(-
 )•
)• =-
=-
(3)由(2)知cn=n

Sn=
 +2×
+2× +3×
+3× +…+n
+…+n ①
① Sn=
Sn= +2×
+2× +…+(n-1)
+…+(n-1) +n
+n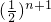 ②
②①-②得:
 Sn=
Sn= +
+ +
+ +…+
+…+ -n
-n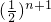
=
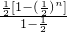 -n•
-n• =1-
=1- -
-
∴Sn=2-
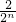 -
- =2-
=2-
∴Sn-2=-

分析:(1)分别将n=1,2,3,4代入到an+1=
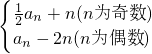 中即可得到a2,a3,a4的值.
中即可得到a2,a3,a4的值.(2)根据bn=a2n-2,然后进行整理即可得到bn+1=
 bn,从而证明数列{bn}是等比数列,进而可求出数列{bn}的通项公式.
bn,从而证明数列{bn}是等比数列,进而可求出数列{bn}的通项公式.(3)先根据(2)中{bn}的通项公式求出 Cn=-nbn,利用错位相减法求得数列{Cn}的前n项和,进而求得Sn-2.
点评:此题考查了有数列的递推关系求前4项的数值,等比数列的定义及通项公式,错位相减法求数列的前n项和,考查运算能力,属中档题.

练习册系列答案
相关题目