Question

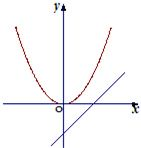在直线y=x-2上是否存在点P，使得经过点P能作出抛物线y=

1

2

x2的两条互相垂直的切线？若存在，求点P的坐标；若不存在，请说明理由．

Answer 1

分析：假设这样的点P存在，由题意可设点P坐标为P（m，m-2），又设所作的两条切线为PA，PB，其中A，B为切点，且点A，B的坐标分别为：A(a，

1

2

a2)，B(b，

1

2

b2)．因为函数y=

1

2

x2的导函数为y'=x，所以由两切线垂直可得ab=-1，由此能够推导出存在这样的点P，其坐标为P(

3

2

，-

1

2

)．

解答：解：假设这样的点P存在，由题意可设点P坐标为P（m，m-2），又设所作的两条切线为PA，PB，其中A，B为切点，且点A，B的坐标分别为：A(a，

1

2

a2)，B(b，

1

2

b2)．
因为函数y=

1

2

x2的导函数为y'=x，
所以由两切线垂直可得ab=-1，
且：

1 2 a2-(m-2) a-m =a 1 2 b2-(m-2) b-m =b

即，

a2-2ma+2(m-2)=0 b2-2mb+2(m-2)=0

．
故a，b是方程x²-2mx+2（m-2）=0的两实数根，
从而有：ab=2（m-2）=-1．解得：m=

3

2

．
所以，存在这样的点P，其坐标为P(

3

2

，-

1

2

)．

点评：本题主要考查直线与圆锥曲线的综合应用能力，具体涉及到轨迹方程的求法及直线与圆、椭圆的相关知识．