题目内容

已知A为圆（x+3）2+（y-2）2=1动点，点B在直线y=x+2上运动，定点P的坐标为（-1，3），则|AB|+|PB|的最小值是
17
-1
17
-1
．
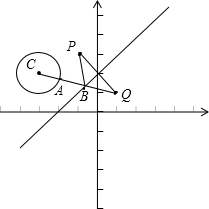
分析：作点P关于直线y=x+2的对称点Q，并连接圆心C交直线于点B，交圆于点A，此时，|AB|+|PB|取得最小值，|QA|即为所求．
解答：解：设点P关于直线y=x+2的对称点Q（x，y），圆心为 C点，即C（-3，2），则
y+3
2
=
x-1
2
+2
y-3
x+1
=-1
解得
x=1
y=1
       
即Q（1，此时|AB|+|PB|的最小值即为|QA|=
17
-1  
故答案应为
17
-1．    
点评：此题考查点关于直线对称及与圆相关最值问题，此类问题一般思路是找三点共线，与圆有关时一般要过圆心．
练习册系列答案
相关题目
已知P为椭圆
x2
25
+
y2
16
=1上的一点，M，N分别为圆（x+3）2+y2=1和圆（x-3）2+y2=4上的点，则|PM|+|PN|的最小值为（　　）
A、5B、7C、13D、15
已知a为实数，p：点M（1，1）在圆（x+a）2+（y-a）2=4的内部； q：?x∈R，都有x2+ax+1≥0．
（1）若p为真命题，求a的取值范围；
（2）若q为假命题，求a的取值范围；
（3）若“p且q”为假命题，且“p或q”为真命题，求a的取值范围．

 

A．（几何证明选讲选做题）

如图，已知AB为圆O的直径，BC切圆O于点B，AC交圆O于点P，E为线段BC的中点．求证：OP⊥PE．

B．（矩阵与变换选做题）

已知M＝，N＝，设曲线y＝sinx在矩阵MN对应的变换作用下得到曲线F，求F的方程．

C．（坐标系与参数方程选做题）

在平面直角坐标系xOy中，直线m的参数方程为（t为参数）；在以O为极点、射线Ox为极轴的极坐标系中，曲线C的极坐标方程为ρsinθ＝8cosθ．若直线m与曲线C交于A、B两点，求线段AB的长．

D．（不等式选做题）

设x，y均为正数，且x＞y，求证：2x＋≥2y＋3．

 
已知P为椭圆
x2
25
+
y2
16
=1上的一点，M，N分别为圆（x+3）2+y2=1和圆（x-3）2+y2=4上的点，则|PM|+|PN|的最小值为（　　）
A．5B．7C．13D．15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网