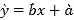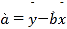题目内容
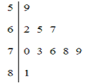
【题目】如图,在直三棱柱![]() 中,
中,![]() ,
,![]() ,M,N分别是
,M,N分别是![]() ,
,![]() 的中点,且
的中点,且![]() .
.

(1)求![]() 的长度;
的长度;
(2)求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)先由题意得到![]() ,建立空间直角坐标系,设
,建立空间直角坐标系,设![]() ,根据
,根据![]() ,用向量的方法,即可求出结果;
,用向量的方法,即可求出结果;
(2)由(1)的结果,用向量的方法求出平面![]() 的一个法向量,以及平面
的一个法向量,以及平面![]() 的一个法向量,由向量夹角公式,求出两法向量的夹角余弦值,即可得出结果.
的一个法向量,由向量夹角公式,求出两法向量的夹角余弦值,即可得出结果.
(1)在![]() 中,
中,![]() ,
,![]() ,
,
则![]() ,所以
,所以![]() .
.
建立如图所示的空间直角坐标系.
设![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() .
.
因为![]() ,
,
所以![]() ,
,
解得![]() ,即
,即![]() 的长为
的长为![]() .
.
(2)由(1)知,![]() ,
,
由N是![]() 的中点,得
的中点,得![]() .
.
所以![]() ,
,![]() .
.
设平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,
,
得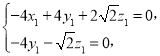 取
取![]() .
.
又![]() ,
,![]() ,
,
设平面![]() 的法向量
的法向量![]() ,
,
由![]() ,
,![]() ,
,
得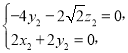 取
取![]() .
.
设平面![]() 与平面
与平面![]() 所成锐二面角的大小为
所成锐二面角的大小为![]() ,
,
则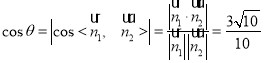 .
.
所以平面![]() 与平面
与平面![]() 所成锐二面角的余弦值为
所成锐二面角的余弦值为![]() .
.

练习册系列答案
相关题目