题目内容
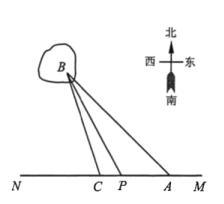
【题目】如图，某沿海地区计划铺设一条电缆联通A，B两地，A地位于东西方向的直线MN上的陆地处，B地位于海上一个灯塔处，在A地用测角器测得
，在A地正西方向4km的点C处，用测角器测得
.拟定铺设方案如下：在岸MN上选一点P，先沿线段AP在地下铺设，再沿线段PB在水下铺设.预算地下、水下的电缆铺设费用分别为2万元/km和4万元/km，设
，
，铺设电缆的总费用为
万元.
（1）求函数的解析式；
（2）试问点P选在何处时，铺设的总费用最少，并说明理由.
【答案】（1）
，其中
（2）当点P选在距离A地
处时，铺设的总费用最少，详见解析.
【解析】
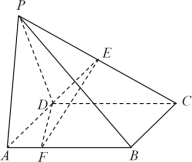
（1）过B作MN的垂线，垂足为D，根据题中条件，得到
，
，由
，得到
，
，
，进而得到
，化简即可得出结果；
（2）根据（1）的结果，先设
，，对
求导，用导数的方法研究其单调性，即可求出最值.
（1）过B作MN的垂线，垂足为D.
在
中，
，则.
在
中，
，
所以.
因为
，所以
，
所以
.
由，则，.
由
，得.
所以，
即，其中.
（2）设，，
则
.
令
，得
，所以
.
列表如下：
|
|
|
|
|
| 0 |
|
h(θ) | ↘ | 极小值 | ↗ |
所以当时，取得最小值
，
所以
取得最小值
，此时
.
答：当点P选在距离A地处时，铺设的总费用最少，且为万元.
53天天练系列答案
【题目】某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下：
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
（1）根据已有数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关？
（3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位女教师的概率.
附：
，
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究，12月1日至12月5日的昼夜温差与实验室每天每100颗种子中的发芽数如下表所示：
日期 | 12月1日 | 12月2日 | 12月3日 | 12月4日 | 12月5日 |
温差x(℃) | 10 | 11 | 13 | 12 | 8 |
发芽数y(颗) | 23 | 25 | 30 | 26 | 16 |
该农科所确定的研究方案是：先从这5组数据中选取2组，用剩下的3组数据求回归方程，再用被选取的2组数据进行检验．
(1)求选取的2组数据恰好是不相邻的2组数据的概率．
(2)若选取的是12月1日与12月5日的两组数据，请根据12月2日至12月4日的数据，求y关于x的线性回归方程
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差不超过2颗，则认为得到的线性回归方程是可靠的，试问(2)中所得的线性回归方程是否可靠？
