题目内容
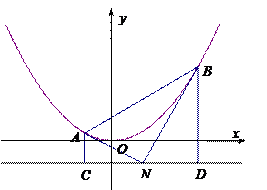
若直线y=kx-2与抛物线y2=8x交于A、B两点,且AB中点的横坐标为2,求k的值.
2
∵直线y=kx-2与抛物线y2=8x交于两点,∴k≠0,
由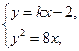 得k2x2-4kx-8x+4=0,∴x1+x2=
得k2x2-4kx-8x+4=0,∴x1+x2=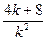 ,
,
而A、B中点横坐标为2,∴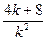 =4,解得k=-1或k=2。
=4,解得k=-1或k=2。
又因为当k=-1时,方程k2x2-4kx-8x+4=0只有一个解,即A、B两点重合,∴k≠-1,
综上所述: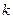 的值为2.
的值为2.
由
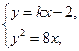 得k2x2-4kx-8x+4=0,∴x1+x2=
得k2x2-4kx-8x+4=0,∴x1+x2=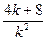 ,
,而A、B中点横坐标为2,∴
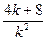 =4,解得k=-1或k=2。
=4,解得k=-1或k=2。又因为当k=-1时,方程k2x2-4kx-8x+4=0只有一个解,即A、B两点重合,∴k≠-1,
综上所述:
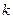 的值为2.
的值为2.
练习册系列答案
相关题目
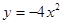 的准线方程是
的准线方程是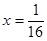
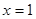
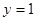
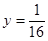
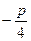 (p>0),顶点在原点,抛物线C与直线l:y =x-1相交所得弦的长为3
(p>0),顶点在原点,抛物线C与直线l:y =x-1相交所得弦的长为3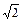 ,求
,求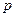 的值和抛物线方程.
的值和抛物线方程.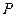 到点
到点 的距离比它到直线
的距离比它到直线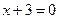 的距离小1,则点
的距离小1,则点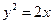



 1的直线过抛物线
1的直线过抛物线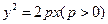 的焦点,与抛物线交于两点
的焦点,与抛物线交于两点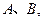 将
将 直线
直线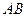 按向量
按向量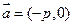 平移到
平移到
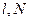 为
为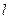 上的动点.(1)若
上的动点.(1)若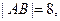 求抛物线的方程;
求抛物线的方程;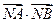 的最小值.
的最小值.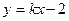 相交于不同的两点A、B,且AB中点横坐标为2,
相交于不同的两点A、B,且AB中点横坐标为2, )
) )
)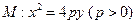 的准线为
的准线为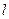 ,
,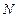 为
为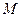 的两条切线,切点分别为
的两条切线,切点分别为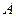 ,
,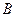 ,再分别过
,再分别过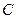 ,
,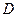 .
.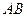 必经过
必经过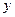 轴上的一个定点
轴上的一个定点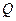 ,并写出点
,并写出点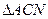 ,
,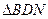 ,
,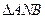 的面积依次构成等差数列,求此时点
的面积依次构成等差数列,求此时点