题目内容
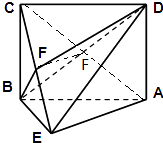
【题目】已知如图:四边形ABCD是矩形,BC⊥平面ABE,且AE=2 ![]() ,EB=BC=2,点F为CE上一点,且BF⊥平面ACE.
,EB=BC=2,点F为CE上一点,且BF⊥平面ACE. 
(1)求证:AE∥平面BFD;
(2)求三棱锥A﹣DBE的体积;
(3)求二面角D﹣BE﹣A的大小.
【答案】
(1)证明:连接AC交BD于G,连结GF,
∵ABCD是矩形,∴G为AC的中点,
由BF⊥平面ACE得:BF⊥CE,
由EB=BC知:点F为CE中点,
∴FG为△ACE的中位线,
∴FG∥AE,
∵AE平面BFD,FG平面BFD,
∴AE∥平面BFD.
(2)解:由BF⊥平面ACE得:BF⊥AE,
由BC⊥平面ABE及BC∥AD,得:BC⊥AE,AD⊥平面ABE,
∵BC∩BF=F,∴AE⊥平面BCE,则AE⊥BE,
∴VA﹣DBE=VD﹣ABE= ![]() ,
,
即三棱锥A﹣DBE的体积为 ![]() .
.
(3)解:由(2)知:AE⊥BE,AD⊥BE,
∴BE⊥平面ADE,则BE⊥DE,
∴∠DEA是二面角D﹣BE﹣A的平面角
在Rt△ADE中,DE= ![]() =4,
=4,
∴AD= ![]() DE,则∠DEA=30°,
DE,则∠DEA=30°,
∴二面角D﹣BE﹣A的大小为30°
【解析】(1)连接AC交BD于G,连结GF,则G为AC的中点,推导出BF⊥CE,FG为△ACE的中位线,由此能证明AE∥平面BFD.(2)推导出BF⊥AE,BC⊥AE,AD⊥平面ABE,从而AE⊥BE,由VA﹣DBE=VD﹣ABE , 能求出三棱锥A﹣DBE的体积.(3)由AE⊥BE,AD⊥BE,得到∠DEA是二面角D﹣BE﹣A的平面角,由此能求出二面角D﹣BE﹣A的大小.
【考点精析】根据题目的已知条件,利用直线与平面平行的判定的相关知识可以得到问题的答案,需要掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行.

 阅读快车系列答案
阅读快车系列答案