Question

【题目】在四棱锥S﹣ABCD中，SA⊥面ABCD，若四边形ABCD为边长为2的正方形，SA=3，则此四棱锥外接球的表面积为 ．

Answer 1

【答案】17π
【解析】解：如图所示
连接AC，BD相交于点O1 ． 取SC的中点，连接OO1 ．
则OO1∥SA．
∵SA⊥底面ABCD，
∴OO1⊥底面ABCD．
可得点O是四棱锥S﹣ABCD外接球的球心．
因此SC是外接球的直径．
∵SC2=SA2+AC2=9+8=17，∴4R2=17，
∴四棱锥P﹣ABCD外接球的表面积为4πR2=π17=17π．
所以答案是：17π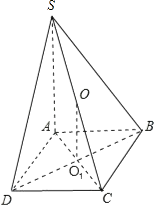

【考点精析】关于本题考查的球内接多面体，需要了解球的内接正方体的对角线等于球直径;长方体的外接球的直径是长方体的体对角线长才能得出正确答案．