题目内容
9．已知sin（α-$\frac{π}{4}$）=$\frac{1}{3}$，则cos（$\frac{π}{4}$+α）的值等于（ ）| A． | $-\frac{1}{3}$ | B． | $\frac{1}{3}$ | C． | $-\frac{{2\sqrt{2}}}{3}$ | D． | $\frac{{2\sqrt{2}}}{3}$ |
分析 运用诱导公式即可化简求值．
解答 解：∵sin（α-$\frac{π}{4}$）=$\frac{1}{3}$，
∴cos（$\frac{π}{4}$+α）=sin[$\frac{π}{2}$-（$\frac{π}{4}$+α）]=sin（$\frac{π}{4}$-α）=-sin（α-$\frac{π}{4}$）=-$\frac{1}{3}$．
故选：A．
点评 本题主要考查了诱导公式的应用，属于基础题．
练习册系列答案
相关题目
19．某工厂为了对新研发的一种产品进行合理定价，将该产品按事先拟定的价格进行试销，得到如下数据：
（Ⅰ）求线性回归方程$\widehat{y}$=bx+a；
（Ⅱ）预计在今后的销售中，销量与单价仍然服从（Ⅰ）中的关系，且该产品的成本是3.5元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）．
（参考公式与数据：$\sum_{i=1}^{6}$xiyi=4066，$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=434.2，$\sum_{i=1}^{6}$xi=51.$\sum_{i=1}^{6}$yi=480.$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．）
| 单价x（元） | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量y（件） | 90 | 84 | 83 | 80 | 75 | 68 |
（Ⅱ）预计在今后的销售中，销量与单价仍然服从（Ⅰ）中的关系，且该产品的成本是3.5元/件，为使工厂获得最大利润，该产品的单价应定为多少元？（利润=销售收入-成本）．
（参考公式与数据：$\sum_{i=1}^{6}$xiyi=4066，$\sum_{i=1}^{6}$x${\;}_{i}^{2}$=434.2，$\sum_{i=1}^{6}$xi=51.$\sum_{i=1}^{6}$yi=480.$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$．）
20．在等比数列{an}中，a1=2，a4=$\frac{1}{4}$．若am=2-15，则m=（ ）
| A． | 17 | B． | 16 | C． | 14 | D． | 13 |
14．若f（x）=|lgx|，当a＜b＜c时，f（a）＞f（c）＞f（b）．则下列不等式中正确的为（ ）
| A． | （a-1）（c-1）＞0 | B． | ac＞1 | C． | ac=1 | D． | ac＜1 |
的单调递增区间是（ ）
B．
C．
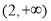D．