题目内容
(本小题满分12分)函数f(x)对任意的实数m,n,有f(m+n)=f(m)+f(n),当x>0时,有f(x)>0。
①求证: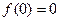
②求证:f(x)在(-∞,+∞)上为增函数.
③若f(1)=1,解不等式f(4x-2x)<2.
①求证:
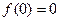
②求证:f(x)在(-∞,+∞)上为增函数.
③若f(1)=1,解不等式f(4x-2x)<2.
①证明略;
②证明略.
③{x|x<1}
②证明略.
③{x|x<1}
①令 ,则
,则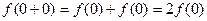
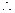
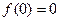 (3分)
(3分)
②令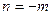 ,则
,则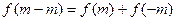
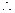
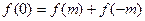
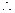
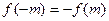
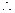
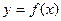 是奇函数。
是奇函数。
在(-∞,+∞)上任取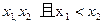 则
则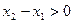
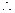
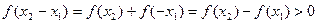
即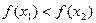
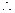 函数
函数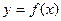 是增函数 (8分)
是增函数 (8分)
③原不等式可化为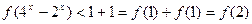
由②得: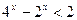 ,
,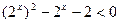
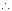
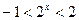 又
又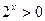 ,
,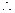
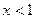
故,原不等式的解集为{x|x<1}. (12分)
 ,则
,则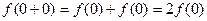
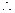
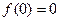 (3分)
(3分)②令
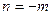 ,则
,则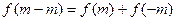
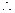
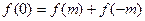
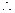
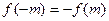
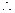
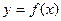 是奇函数。
是奇函数。在(-∞,+∞)上任取
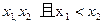 则
则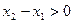
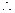
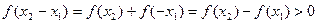
即
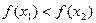
 函数
函数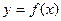 是增函数 (8分)
是增函数 (8分)③原不等式可化为
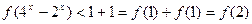
由②得:
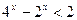 ,
,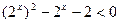
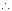
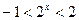 又
又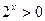 ,
,
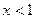
故,原不等式的解集为{x|x<1}. (12分)

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
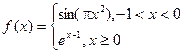 ,若
,若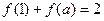 ,则
,则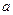 的所有可能值为___________.
的所有可能值为___________.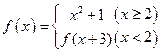 ,则
,则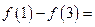 ( )
( )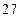
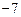
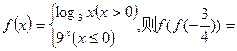 ______________
______________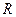 上的函数
上的函数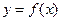 满足
满足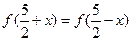 ,
,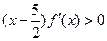 ,任意的
,任意的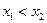 ,都有
,都有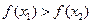 是
是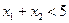 的( )条件.
的( )条件.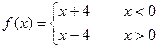 ,则
,则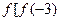 ]的值为 ( )
]的值为 ( )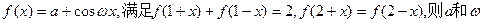 的一组值是 ( )
的一组值是 ( )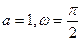
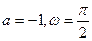
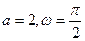
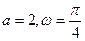
 已知函数
已知函数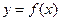 是R上的偶函数,对于
是R上的偶函数,对于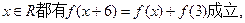
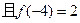 ,当
,当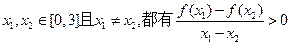 ,则给出下列命题:
,则给出下列命题: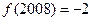 ;②函数
;②函数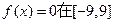 上有4个根,其中正确的命题序号为 。
上有4个根,其中正确的命题序号为 。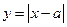 的图象关于直线
的图象关于直线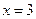 对称.则
对称.则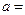 _____________.
_____________.