题目内容
【题目】某高校组织自主招生考试,其有2 000名学生报名参加了笔试,成绩均介于195分到275分之间,从中随机抽取50名同学的成绩进行统计,将统计结果按如下方式分成八组:第一组[195,205),第二组[205,215),…,第八组[265,275).如图是按上述分组方法得到的频率分布直方图. 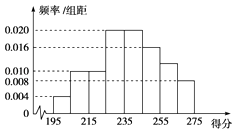
(1)从这2 000名学生中,任取1人,求这个人的分数在255~265之间的概率约是多少?
(2)求这2 000名学生的平均分数;
(3)若计划按成绩取1 000名学生进入面试环节,试估计应将分数线定为多少?
【答案】
(1)解:由频率分布直方图得分数在255~265之间的频率为:
1﹣(0.004+0.010×2+0.020×2+0.0165+0.008)×10=0.12.
∴从这2 000名学生中,任取1人,这个人的分数在255~265之间的概率约是0.12.
(2)解:由频率分布直方图的性质得:
这2 000名学生的平均分数为:
200×0.004×10+210×0.010×10+220×0.010×10+230×0.020×10+240×0.020×10+250×0.016×10+260×0.12+270×0.008×10=237.8.
(3)解:从第一组到第四组,频率为0.04+0.1+0.1+0.2=0.44,而0.5﹣0.44=0.06,
将第五组[235,245),按以下比例分割: ![]() =
= ![]() ,
,
∴中位数为235+3=238,
∴计划按成绩取1 000名学生进入面试环节,应将分数线定为238分.
【解析】(1)由频率分布直方图求出分数在255~265之间的频率,由此能出从这2 000名学生中,任取1人,这个人的分数在255~265之间的概率.(2)由频率分布直方图的性质能求出这2 000名学生的平均分数.(3)由频率分布直方图的性质能求出中位数,由此能出计划按成绩取1 000名学生进入面试环节,应将分数线定为多少分.
【考点精析】认真审题,首先需要了解频率分布直方图(频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息),还要掌握平均数、中位数、众数(⑴平均数、众数和中位数都是描述一组数据集中趋势的量;⑵平均数、众数和中位数都有单位;⑶平均数反映一组数据的平均水平,与这组数据中的每个数都有关系,所以最为重要,应用最广;⑷中位数不受个别偏大或偏小数据的影响;⑸众数与各组数据出现的频数有关,不受个别数据的影响,有时是我们最为关心的数据)的相关知识才是答题的关键.

【题目】某地最近十年对某商品的需求量逐年上升,下表是部分统计数据:
年份 | 2008 | 2010 | 2012 | 2014 | 2016 |
需要量(万件) | 236 | 246 | 257 | 276 | 286 |
(1)利用所给数据求年需求量y与年份x之间的回归直线方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)预测该地2018年的商品需求量(结果保留整数).