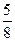题目内容
设不等式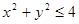 确定的平面区域为
确定的平面区域为 ,
,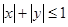 确定的平面区域为
确定的平面区域为
(1)定义横、纵坐标为整数的点为“整点”,在区域 内任取
内任取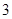 个整点,求这些整点中恰有
个整点,求这些整点中恰有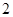 个整点在区域
个整点在区域 内的概率;
内的概率;
(2)在区域 内任取
内任取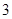 个点,记这
个点,记这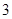 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望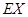 及方差
及方差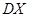 .
.
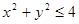 确定的平面区域为
确定的平面区域为 ,
,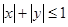 确定的平面区域为
确定的平面区域为
(1)定义横、纵坐标为整数的点为“整点”,在区域
 内任取
内任取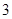 个整点,求这些整点中恰有
个整点,求这些整点中恰有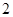 个整点在区域
个整点在区域 内的概率;
内的概率;(2)在区域
 内任取
内任取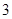 个点,记这
个点,记这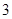 个点在区域
个点在区域 内的个数为
内的个数为 ,求
,求 的分布列,数学期望
的分布列,数学期望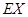 及方差
及方差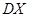 .
.(1)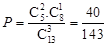 .(2)
.(2) 的分布列为:
的分布列为:
 的数学期望
的数学期望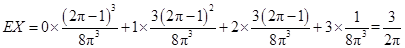 .
.
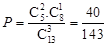 .(2)
.(2) 的分布列为:
的分布列为:   | 0 | 1 | 2 | 3 |
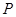 | 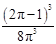 | 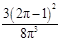 | 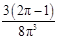 | 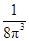 |
 的数学期望
的数学期望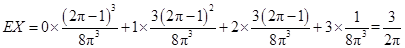 .
.(1)由题意知本题是一个古典概型,用列举法求出平面区域U的整点的个数N,平面区域V的整点个数为n,这些整点中恰有2个整点在区域V的概率
(1)依题可得:平面区域U的面积为:π•22=4π,平面区域V的面积为: ×2×2=2,在区域U内任取1个点,则该点在区域V内的概率为
×2×2=2,在区域U内任取1个点,则该点在区域V内的概率为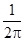
易知:X的可能取值为0,1,2,3,则X∽B(3,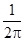 ) ,代入概率公式即可求得求X的分布列和数学期望和方差
) ,代入概率公式即可求得求X的分布列和数学期望和方差
(1)依题可知平面区域 的整点有
的整点有
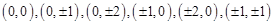 共有13个, ……2分
共有13个, ……2分
平面区域 的整点为
的整点为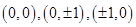 共有5个,∴
共有5个,∴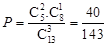 .……4分
.……4分
(2)依题可得:平面区域 的面积为:
的面积为: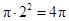 ,平面区域
,平面区域 的面积为:
的面积为: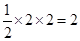 .
.
在区域 内任取1个点,则该点在区域
内任取1个点,则该点在区域 内的概率为
内的概率为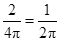 , ……1分
, ……1分
法一:显然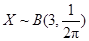 ,则
,则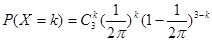 ,
,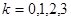 ……3分
……3分
∴ 的分布列为:
的分布列为:
故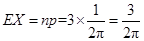 ,
,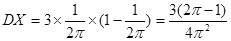 ……3分
……3分
法二: 的可能取值为
的可能取值为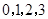 ,
,

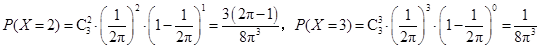 .
.
∴ 的分布列为:
的分布列为:
 的数学期望
的数学期望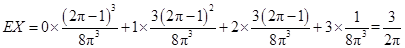
(1)依题可得:平面区域U的面积为:π•22=4π,平面区域V的面积为:
 ×2×2=2,在区域U内任取1个点,则该点在区域V内的概率为
×2×2=2,在区域U内任取1个点,则该点在区域V内的概率为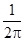
易知:X的可能取值为0,1,2,3,则X∽B(3,
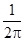 ) ,代入概率公式即可求得求X的分布列和数学期望和方差
) ,代入概率公式即可求得求X的分布列和数学期望和方差(1)依题可知平面区域
 的整点有
的整点有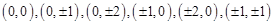 共有13个, ……2分
共有13个, ……2分平面区域
 的整点为
的整点为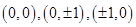 共有5个,∴
共有5个,∴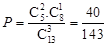 .……4分
.……4分(2)依题可得:平面区域
 的面积为:
的面积为: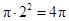 ,平面区域
,平面区域 的面积为:
的面积为: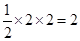 .
.在区域
 内任取1个点,则该点在区域
内任取1个点,则该点在区域 内的概率为
内的概率为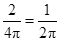 , ……1分
, ……1分 法一:显然
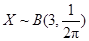 ,则
,则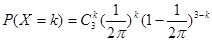 ,
,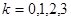 ……3分
……3分∴
 的分布列为:
的分布列为:   | 0 | 1 | 2 | 3 |
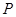 | 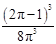 | 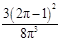 | 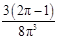 | 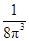 |
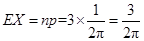 ,
,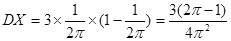 ……3分
……3分法二:
 的可能取值为
的可能取值为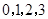 ,
, 
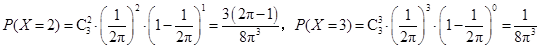 .
.∴
 的分布列为:
的分布列为:   | 0 | 1 | 2 | 3 |
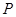 | 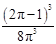 | 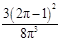 | 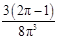 | 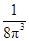 |
 的数学期望
的数学期望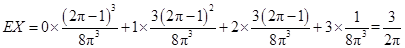

练习册系列答案
相关题目
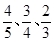 ,在实际操作考试中“合格”的概率依次为
,在实际操作考试中“合格”的概率依次为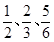 ,所有考试是否合格相互之间没有影响。
,所有考试是否合格相互之间没有影响。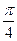 ;
;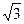 。
。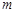 和
和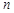 ,则复数
,则复数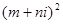 为纯虚数的概率为( )
为纯虚数的概率为( ) 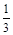
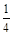

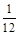
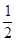 和
和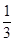 , 甲、乙两人各射击一次,有下列说法: ① 目标恰好被命中一次的概率为
, 甲、乙两人各射击一次,有下列说法: ① 目标恰好被命中一次的概率为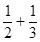 ;② 目标恰好被命中两次的概率为
;② 目标恰好被命中两次的概率为 ; ③ 目标被命中的概率为
; ③ 目标被命中的概率为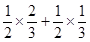 ; ④ 目标被命中的概率为
; ④ 目标被命中的概率为 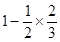 。以上说法正确的序号依次是
。以上说法正确的序号依次是 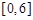 内任取两个数(可以相等),分别记为
内任取两个数(可以相等),分别记为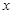 和
和 ,
,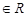 ,求
,求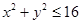 的概率.
的概率. ,乙解出它的概率为
,乙解出它的概率为 ,丙解出它的概率为
,丙解出它的概率为 ,则
,则 B.
B. C.
C.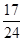 D.1
D.1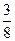 B.
B.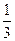
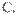
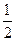 D.
D.