题目内容
在区间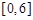 内任取两个数(可以相等),分别记为
内任取两个数(可以相等),分别记为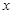 和
和 ,
,
(1)若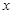 、
、 为正整数,求这两数中至少有一个偶数的概率;
为正整数,求这两数中至少有一个偶数的概率;
(2)若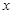 、
、
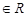 ,求
,求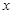 、
、 满足
满足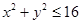 的概率.
的概率.
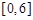 内任取两个数(可以相等),分别记为
内任取两个数(可以相等),分别记为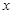 和
和 ,
,(1)若
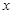 、
、 为正整数,求这两数中至少有一个偶数的概率;
为正整数,求这两数中至少有一个偶数的概率;(2)若
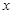 、
、
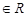 ,求
,求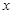 、
、 满足
满足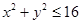 的概率.
的概率.(1) 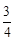 ;(2)
;(2) 
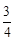 ;(2)
;(2) 
本试题主要是考查而来古典概型概率的计算,以及几何概型概率的求解的综合运用。
(1)因为当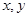 为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,“两个数
为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,“两个数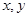 中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,利用概率公式解得
中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,利用概率公式解得
(2)当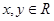 时,记事件总体为
时,记事件总体为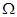 ,所求事件为B,则有
,所求事件为B,则有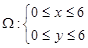 , B:
, B: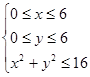 ,
,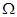 对应的区域为正方形,其面积为
对应的区域为正方形,其面积为 ,B对应的区域为四分之一圆,其面积为
,B对应的区域为四分之一圆,其面积为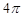 ,则由几何概型知道结论。
,则由几何概型知道结论。
解:(1)当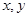 为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,如下:
为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,如下:
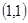 、
、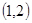 、
、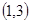 、
、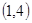 、
、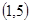 、
、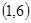 ;
;  、
、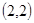 、
、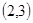 、
、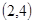 、
、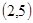 、
、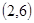 ;
;
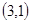 、
、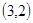 、
、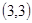 、
、 、
、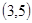 、
、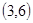 ;
; 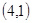 、
、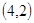 、
、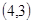 、
、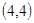 、
、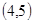 、
、 ;
;
 、
、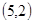 、
、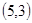 、
、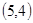 、
、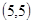 、
、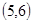 ;
; 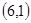 、
、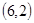 、
、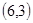 、
、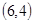 、
、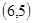 、
、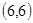 .
.
记“两个数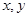 中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,由古典概型可知
中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,由古典概型可知 .
.  分
分
(2)当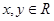 时,记事件总体为
时,记事件总体为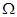 ,所求事件为B,则有
,所求事件为B,则有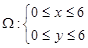 , B:
, B: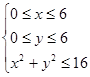 ,
,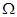 对应的区域为正方形,其面积为
对应的区域为正方形,其面积为 ,B对应的区域为四分之一圆,其面积为
,B对应的区域为四分之一圆,其面积为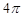 ,由几何概型可知
,由几何概型可知 .
.  分
分
(1)因为当
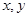 为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,“两个数
为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,“两个数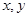 中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,利用概率公式解得
中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,利用概率公式解得(2)当
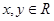 时,记事件总体为
时,记事件总体为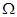 ,所求事件为B,则有
,所求事件为B,则有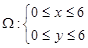 , B:
, B: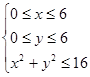 ,
,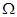 对应的区域为正方形,其面积为
对应的区域为正方形,其面积为 ,B对应的区域为四分之一圆,其面积为
,B对应的区域为四分之一圆,其面积为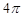 ,则由几何概型知道结论。
,则由几何概型知道结论。解:(1)当
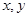 为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,如下:
为正整数,同时抛掷两枚骰子,等可能性的基本事件共36个,如下: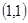 、
、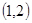 、
、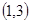 、
、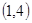 、
、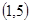 、
、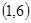 ;
;  、
、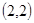 、
、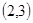 、
、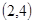 、
、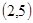 、
、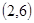 ;
;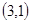 、
、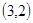 、
、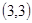 、
、 、
、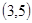 、
、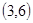 ;
; 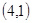 、
、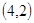 、
、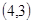 、
、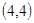 、
、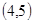 、
、 ;
; 、
、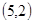 、
、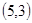 、
、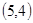 、
、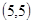 、
、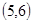 ;
; 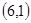 、
、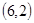 、
、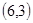 、
、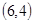 、
、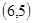 、
、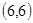 .
.记“两个数
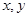 中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,由古典概型可知
中至少有一个为偶数”为事件A,包含上述基本事件的个数为27,由古典概型可知 .
. 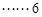 分
分(2)当
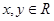 时,记事件总体为
时,记事件总体为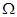 ,所求事件为B,则有
,所求事件为B,则有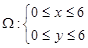 , B:
, B: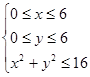 ,
,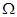 对应的区域为正方形,其面积为
对应的区域为正方形,其面积为 ,B对应的区域为四分之一圆,其面积为
,B对应的区域为四分之一圆,其面积为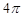 ,由几何概型可知
,由几何概型可知 .
. 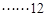 分
分
练习册系列答案
相关题目
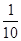 ,不堵车的概率为
,不堵车的概率为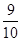 ;走公路Ⅱ堵车的概率为
;走公路Ⅱ堵车的概率为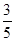 ,不堵车的概率为
,不堵车的概率为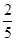 ,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.
,若甲、乙两辆汽车走公路Ⅰ,第三辆汽车丙由于其他原因走公路Ⅱ运送水果,且三辆汽车是否堵车相互之间没有影响.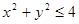 确定的平面区域为
确定的平面区域为 ,
,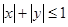 确定的平面区域为
确定的平面区域为
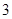 个整点,求这些整点中恰有
个整点,求这些整点中恰有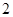 个整点在区域
个整点在区域 ,求
,求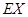 及方差
及方差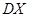 .
.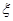 ,求
,求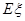 (即均值).
(即均值).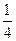 ,不堵车的概率为
,不堵车的概率为 ;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。
;汽车走公路②堵车的概率为p,不堵车的概率为1—p。若甲、乙两辆汽车走公路①,丙汽车由于其他原因走公路②,且三辆车是否堵车相互之间没有影响。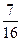 ,求走公路②堵的概率;
,求走公路②堵的概率;