题目内容
试从几何变换的角度求AB的逆矩阵.
(1)A=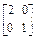 ,B=
,B=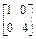 ;
;
(2)A=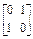 ,B=
,B=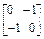 .
.
(1)A=
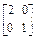 ,B=
,B=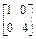 ;
;(2)A=
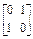 ,B=
,B=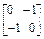 .
.(1)(AB)-1=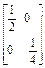 (2)(AB)-1=
(2)(AB)-1=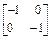 .
.
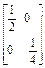 (2)(AB)-1=
(2)(AB)-1=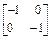 .
.(1)矩阵A对应的是伸压变换,它将平面内的点的纵坐标保持不变,横坐标伸长为原来的2倍,因此它的逆矩阵是A-1=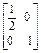 ;
;
同理,矩阵B对应的也是伸压变换,它将平面内的点的横坐标保持不变,纵坐标伸长为原来的4倍,因此它的逆矩阵是
B-1=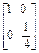 ;
;
所以(AB)-1=B-1A-1=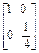 ·
·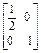 =
=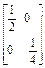 .
.
(2)矩阵A对应的是反射变换,它将平面内的点变为该点关于直线x-y=0的对称点,所以该变换的逆变换为其自身,A-1=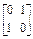 ;
;
矩阵B对应的也是反射变换,它将平面内的点变换为与其关于原点对称的点,
所以B-1=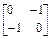 ;
;
所以,(AB)-1=B-1A-1=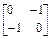
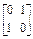 =
=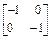 .
.
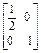 ;
;同理,矩阵B对应的也是伸压变换,它将平面内的点的横坐标保持不变,纵坐标伸长为原来的4倍,因此它的逆矩阵是
B-1=
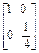 ;
;所以(AB)-1=B-1A-1=
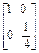 ·
·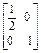 =
=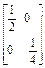 .
.(2)矩阵A对应的是反射变换,它将平面内的点变为该点关于直线x-y=0的对称点,所以该变换的逆变换为其自身,A-1=
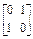 ;
;矩阵B对应的也是反射变换,它将平面内的点变换为与其关于原点对称的点,
所以B-1=
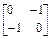 ;
;所以,(AB)-1=B-1A-1=
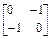
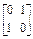 =
=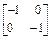 .
.
练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
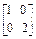 ,N=
,N=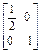 .
.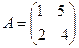 ,求A的特征值以及属于每个特征值的一个特征向量。
,求A的特征值以及属于每个特征值的一个特征向量。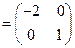 的特征值和特征向量.
的特征值和特征向量. ,该方程组的解为
,该方程组的解为 则
则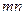
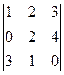 中第二行第一列元素0的代数余子式是________.
中第二行第一列元素0的代数余子式是________. 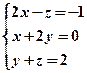 的增广矩阵是__________________.
的增广矩阵是__________________.