题目内容
求出矩阵A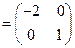 的特征值和特征向量.
的特征值和特征向量.
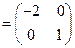 的特征值和特征向量.
的特征值和特征向量.矩阵A的特征值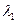 =-2,
=-2,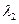
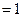 ;属于特征值-2的特征向量为
;属于特征值-2的特征向量为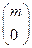 ,属于特征值1的特征向量为
,属于特征值1的特征向量为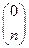 。
。
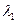 =-2,
=-2,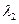
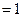 ;属于特征值-2的特征向量为
;属于特征值-2的特征向量为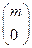 ,属于特征值1的特征向量为
,属于特征值1的特征向量为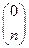 。
。特征矩阵为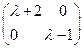 ,特征多项式
,特征多项式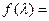
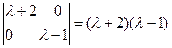 ,
,
令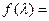 0,解得矩阵A的特征值
0,解得矩阵A的特征值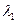 =-2,
=-2,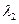
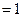 ,
,
将 -2代入特征矩阵得
-2代入特征矩阵得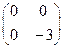 ,
,
以它为系数矩阵的二元一次方程组是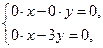
解之得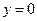 ,
,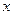 可以为任何非零实数,不妨记
可以为任何非零实数,不妨记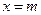 (
(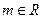 ,
,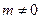 ),于是,矩阵A的属于特征值-2的特征向量为
),于是,矩阵A的属于特征值-2的特征向量为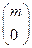 .
.
再将 1代入特征矩阵得
1代入特征矩阵得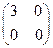 ,
,
以它为系数矩阵的二元一次方程组是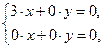
解之得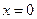 ,
,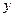 可以为任何非零实数,记
可以为任何非零实数,记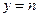 (
(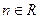 ,
,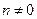 ),于是矩阵A的属于特征值1的特征向量为
),于是矩阵A的属于特征值1的特征向量为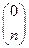 .
.
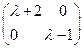 ,特征多项式
,特征多项式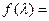
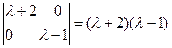 ,
, 令
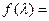 0,解得矩阵A的特征值
0,解得矩阵A的特征值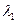 =-2,
=-2,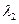
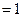 ,
, 将
 -2代入特征矩阵得
-2代入特征矩阵得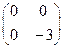 ,
,以它为系数矩阵的二元一次方程组是
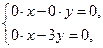
解之得
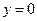 ,
,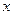 可以为任何非零实数,不妨记
可以为任何非零实数,不妨记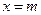 (
(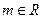 ,
,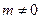 ),于是,矩阵A的属于特征值-2的特征向量为
),于是,矩阵A的属于特征值-2的特征向量为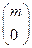 .
. 再将
 1代入特征矩阵得
1代入特征矩阵得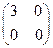 ,
,以它为系数矩阵的二元一次方程组是
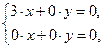
解之得
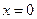 ,
,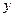 可以为任何非零实数,记
可以为任何非零实数,记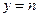 (
(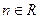 ,
,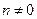 ),于是矩阵A的属于特征值1的特征向量为
),于是矩阵A的属于特征值1的特征向量为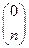 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
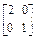 ,B=
,B=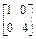 ;
;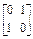 ,B=
,B=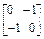 .
.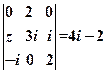 (
(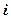 为虚数单位),则复数
为虚数单位),则复数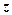 =_______.
=_______.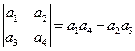 ,将函数
,将函数 的图象向左平移
的图象向左平移 个单位(
个单位(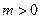 ),若所得图象对应的函数为偶函数,则
),若所得图象对应的函数为偶函数,则