题目内容
甲袋内装有2个红球和3个白球,乙袋内装有1个红球和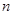
 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
 的判断正确的是
的判断正确的是
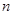
 个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球.现分别从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .则以下关于函数
.则以下关于函数
 的判断正确的是
的判断正确的是A. 有最小值,且最小值为 有最小值,且最小值为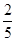 | B. 有最大值,且最大值为 有最大值,且最大值为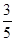 |
C. 有最小值,且最小值为 有最小值,且最小值为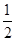 | D. 有最大值,且最大值为 有最大值,且最大值为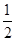 |
C
试题分析:对于甲袋内装有2个红球和3个白球,乙袋内装有1个红球和
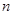
 个白球,那么从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为
个白球,那么从甲、乙两袋中各取1个球,若将事件“取出的2个球恰为同色”发生的概率记为 .可以分为两种情况,都是红球的概率为
.可以分为两种情况,都是红球的概率为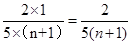 ,都是白球的概率为
,都是白球的概率为 ,那么可知,后者大于前者,并且可知函数有最小值为当n=5时,则可知概率值最小为
,那么可知,后者大于前者,并且可知函数有最小值为当n=5时,则可知概率值最小为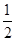 ,故选C.
,故选C.点评:考查了古典概型概率的求解,题目比较常规,分类讨论可知结论。属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
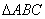 中,
中,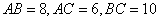 ,顶点
,顶点 处分别有一枚半径为1的硬币(顶点
处分别有一枚半径为1的硬币(顶点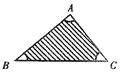
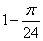
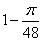
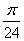
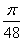
 为( )
为( )



 ,
, ,已知
,已知 =
= ,
,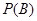 =
=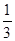 ,
, =
= ,则
,则 等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为
等10所高校举行的自主招生考试,某同学参加每所高校的考试获得通过的概率均为 .
. 元,该同学决定按
元,该同学决定按 的分布列及数学期望.
的分布列及数学期望.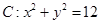 ,直线
,直线 ,圆C上任意一点A到直线
,圆C上任意一点A到直线 的距离小于2的概率为
的距离小于2的概率为

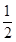
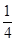




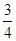 ,谁能将铜板整个扔到方几上,就可以进行下一轮比赛。郭靖一扔,铜板落在小方几上,且没有掉下,问他能进入下一轮比赛的概率多大? ( )
,谁能将铜板整个扔到方几上,就可以进行下一轮比赛。郭靖一扔,铜板落在小方几上,且没有掉下,问他能进入下一轮比赛的概率多大? ( )