题目内容
16.函数f(x)=-(x-$\frac{1}{x}$)cosx(-π≤x≤π且x≠0)的图象可能为( )| A. |  | B. |  | C. |  | D. | 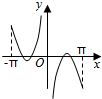 |
分析 由条件可得函数f(x)为奇函数,故它的图象关于原点对称;再根据但是当x趋向于0时,f(x)>0,结合所给的选项,得出结论.
解答 解:对于函数f(x)=-($\frac{1}{x}$-x)cosx(-π≤x≤π且x≠0),由于它的定义域关于原点对称,
且满足f(-x)=-(-$\frac{1}{x}$+x)cosx=($\frac{1}{x}$-x)=-f(x),故函数f(x)为奇函数,故它的图象关于原点对称.
故排除A、B.
当x=π,f(x)>0,故排除D,
但是当x趋向于0时,f(x)>0,
故选:C.
点评 本题主要考查函数的奇偶性的判断,奇函数的图象特征,函数的定义域和值域,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
6. 如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
 如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )
如图,矩形ABCD中,点A在x轴上,点B的坐标为(1,0),且点C与点D在函数f(x)=$\left\{\begin{array}{l}{x+1,}&{x≥0}\\{-\frac{1}{2}x+1,}&{x<0}\end{array}\right.$的图象上,若在矩形ABCD内随机取一点,则此点取自阴影部分的概率等于( )| A. | $\frac{1}{6}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
7.在区间[0,1]上随机取两个数x,y,记P1为事件“x+y≥$\frac{1}{2}$”的概率,P2为事件“|x-y|≤$\frac{1}{2}$”的概率,P3为事件“xy≤$\frac{1}{2}$”的概率,则( )
| A. | P1<P2<P3 | B. | P2<P3<P1 | C. | P3<P1<P2 | D. | P3<P2<P1 |
15.已知等比数列{an}的前n项和为Sn,若S2n=4(a1+a3+…+a2n-1),a1•a2•a3=27,则a6=( )
| A. | 27 | B. | 81 | C. | 243 | D. | 729 |
16.已知i是虚数单位,若复数z满足z=$\frac{25}{3-4i}$,则z的共轭复数$\overline{z}$为( )
| A. | -3+4i | B. | -3-4i | C. | 3+4i | D. | 3-4i |
 如图,已知抛物线C1:y=$\frac{1}{4}$x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.
如图,已知抛物线C1:y=$\frac{1}{4}$x2,圆C2:x2+(y-1)2=1,过点P(t,0)(t>0)作不过原点O的直线PA,PB分别与抛物线C1和圆C2相切,A,B为切点.