题目内容
【题目】如图1,2,在Rt△ABC中,AB=BC=4,点E在线段AB上,过点E作交AC于点F,将△AEF沿EF折起到△PEF的位置(点A与P重合),使得∠PEB=60°. 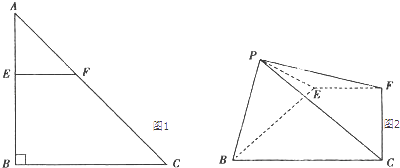
(1)求证:EF⊥PB;
(2)试问:当点E在何处时,四棱锥P﹣EFCB的侧面的面积最大?并求此时四棱锥P﹣EFCB的体积及直线PC与平面EFCB所成角的正切值.
【答案】
(1)证明:∵EF∥BC且BC⊥AB,
∴EF⊥AB,即EF⊥BE,EF⊥PE.又BE∩PE=E,
∴EF⊥平面PBE,又PB平面PBE,
∴EF⊥PB
(2)证明:解:设BE=x,PE=y,则x+y=4.
∴ ![]() .
.
当且仅当x=y=2时,S△PEB的面积最大,此时,BE=PE=2.
由(1)知EF⊥平面PBE,
∵EF平面EFCB,∴平面EFCB⊥平面PBE.
在平面PBE中,作PO⊥BE于O,则PO⊥平面EFCB.
即PO为四棱锥P﹣EFCB的高.
又 ![]() .
.
∴ ![]()
∵ ![]() ,
,
∴BO=1,在Rt△OBC中, ![]() .
.
∵PO⊥平面EFCB,∴∠PCO就是PC与平面EFCB所成角.
∴ ![]() ,
,
故直线PC与平面EFCB所成角的正切值为 ![]()
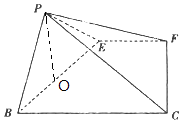
【解析】(1)推导出EF⊥AB,EF⊥BE,EF⊥PE,由此能证明EF⊥PB. (2)设BE=x,PE=y,则x+y=4,当且仅当x=y=2时,S△PEB的面积最大,此时,BE=PE=2.EF⊥平面PBE,从而平面EFCB⊥平面PBE.作PO⊥BE于O,则PO为四棱锥P﹣EFCB的高,∠PCO就是PC与平面EFCB所成角.由此能求出结果.
【考点精析】掌握空间中直线与直线之间的位置关系和空间角的异面直线所成的角是解答本题的根本,需要知道相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则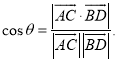 .
.