题目内容
7.设实数x,y满足不等式组$\left\{\begin{array}{l}{1≤x+y≤4}\\{y+2≥|2x-3|}\end{array}\right.$(1)求点(x,y)所在的平面区域.
(2)设-1<a<0,在(1)所求的区域内,求函数f(x,y)=y-ax的最大值和最小值.
分析 (1)将点的坐标设出,据已知求出点的横坐标、纵坐标满足的约束条件,画出可行域,
(2)①观察(1)的可行域②z为目标函数纵截距③画直线y-ax=0,平移直线观察最值.
解答 解:(1)作出满足约束条件的可行域,
如图所示: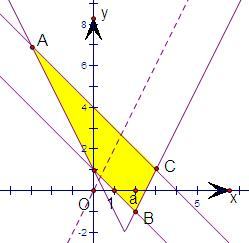
(2)由(1)可知,
当直线z=y-ax的斜率-1<a<0时,
直线z=y-ax平移到点A(-3,7)时,
目标函数z=y-ax取得最大值7+3a;
当直线z=y-ax平移到点B(2,-1)时,
目标函数z=y-ax取得最小值-2a-1;
综上所述:最大值为7+3a,最小值为:-2a-1.
点评 本题考查不等式中的线性规划知识,画出平面区域与正确理解目标函数z=y-ax的几何意义是解答好本题的关键

练习册系列答案
相关题目
15.已知f(x)=$\left\{\begin{array}{l}{a{x}^{2}+2x,x≥0}\\{{x}^{2}+bx,x<0}\end{array}\right.$是奇函数,则a-b的值为( )
| A. | -3 | B. | -2 | C. | -1 | D. | 不能确定 |
19.等差数列{an}中,已知a5+a6=10,则S10=( )
| A. | 30 | B. | 40 | C. | 50 | D. | 60 |
 如图,定圆半径为a,圆心为(b,c),则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.
如图,定圆半径为a,圆心为(b,c),则直线ax+by+c=0与直线x+y+1=0的交点在第二象限.