题目内容
在△ABC中,a、b、c分别是三内角A、B、C的对应的三边,已知csinA=-acosC
(1)求角C的大小;
(2)满足
sinA-cos(B+
)=2的△ABC是否存在?若存在,求角A的大小.
(1)求角C的大小;
(2)满足
| 3 |
| 3π |
| 4 |
(1)由正弦定理,得sinC•sinA=-sinA•cosC,
∵0<A<π,
∴sinA>0,
∴sinC=-cosC,
∵0<C<π,
∴cosC≠0,
∴tanC=-1,
则C=
;
(2)满足
sinA-cos(B+
)=2的△ABC不存在,理由为:
∵A∈(0,
),
∴A+
∈(
,
),
∴sin(A+
)<1,
由(1)知B+
=π-A,得到
sinA-cos(B+
)=
sinA+cosA=2sin(A+
)<2,
∴这样的三角形不存在.
∵0<A<π,
∴sinA>0,
∴sinC=-cosC,
∵0<C<π,
∴cosC≠0,
∴tanC=-1,
则C=
| 3π |
| 4 |
(2)满足
| 3 |
| 3π |
| 4 |
∵A∈(0,
| π |
| 4 |
∴A+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 12 |
∴sin(A+
| π |
| 6 |
由(1)知B+
| 3π |
| 4 |
| 3 |
| 3π |
| 4 |
| 3 |
| π |
| 6 |
∴这样的三角形不存在.

练习册系列答案
相关题目
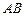 至少长
至少长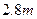 ,
,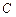 为
为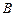 到
到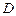 的距离比
的距离比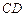 的长小
的长小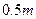 ,
,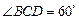 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计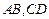 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?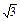 ,b=
,b=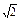 ,B=45°,求A、C和c.
,B=45°,求A、C和c. 则cos A= .
则cos A= .