题目内容
m为何值时,直线x+2y-3=0与圆x2+y2+x-6y+m=0相离?
M的取值范围为 .
.
 .
.将直线方程x=3-2y代入x2+y2+x-6y+m=0得5y2-20y+12+m=0.
∵直线与圆相离,
∴Δ=400-20(12+m)<0,得m>8.
又知方程x2+y2+x-6y+m=0表示圆的条件为D2+E2-4F>0,即37-4m>0,
∴ .
.
故满足条件的M的取值范围为 .
.
∵直线与圆相离,
∴Δ=400-20(12+m)<0,得m>8.
又知方程x2+y2+x-6y+m=0表示圆的条件为D2+E2-4F>0,即37-4m>0,
∴
 .
.故满足条件的M的取值范围为
 .
.
练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 ,求圆心到直线
,求圆心到直线 的距离的取值范围.(14分)
的距离的取值范围.(14分)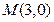 是圆
是圆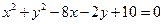 内一点,过
内一点,过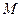 点最长的弦所在的直线的
点最长的弦所在的直线的







 ,则圆的方程为( )
,则圆的方程为( )