Question

【题目】设等差数列{an}的前n项和为Sn，且S4＝4S2，a2n＝2an+1．

（1）求数列{an}的通项公式；

（2）设数列{bn}的前n项和为Tn，且，令cn＝b2n(n∈N*)，求数列{cn}的前n项和Rn．

Answer 1

【答案】(1) an＝2n-1，n∈N*;(2) ．

【解析】试题分析：（1）利用等差数列的通项公式和求和公式，利用基本量法解出，得到通项公式；（2）利用和cn＝b2n解得，利用错位相减法求出。

试题解析：

（1）设等差数列{an}的首项为a1，公差为d．

由S4＝4S2，a2n＝2an+1，得

解得a1＝1，d＝2．

因此an＝2n-1，n∈N*．

（2）由题意知，

所以n≥2时， ，

故，n∈N*．

所以，

则，

两式相减得

，

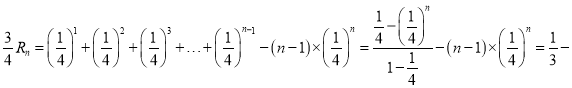
整理得．

所以数列{cn}的前n项和．