题目内容
8.已知角α满足(4k+1)π<α<(4k+1)π+$\frac{π}{6}$(k∈z),那么$\frac{α}{2}$是第二象限角,2α是第一象限角.分析 由(4k+1)π<α<(4k+1)π+$\frac{π}{6}$(k∈z)直接得出$\frac{α}{2}$、2α的范围得答案.
解答 解:由(4k+1)π<α<(4k+1)π+$\frac{π}{6}$(k∈z),得
$2kπ+\frac{π}{2}<\frac{α}{2}<2kπ+\frac{7π}{12}$(k∈z),∴$\frac{α}{2}$是第二象限角;
$(8k+2)π<2α<(8k+2)π+\frac{π}{3}$(k∈z),∴2α是第一象限角.
故答案为:二,一.
点评 本题考查终边相同角的概念,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
20.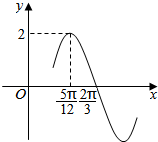 已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
 已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )
已知函数f(x)=2sin(ωx+φ)(ω>0,且|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的一个单调递增区间是( )| A. | [-$\frac{7π}{12}$,$\frac{5π}{12}$] | B. | [-$\frac{7π}{12}$,-$\frac{π}{12}$] | C. | [-$\frac{π}{12}$,$\frac{7π}{12}$] | D. | [-$\frac{π}{12}$,$\frac{5π}{12}$] |